某班级统计一次数学测试后的成绩,并制成了如下的频率分布表,根据该表估计该班级的数学测试平均分为( )
| 分组 |
[60,70) |
[70,80) |
[80,90) |
[90,100) |
| 人数 |
5 |
15 |
20 |
10 |
| 频率 |
0.1 |
0.3 |
0.4 |
0.2 |
A.80 B.81 C.82 D.83
(本小题满分12分)为备战某次运动会,某市体育局组建了一个由4个男运动员和2个女运动员组成的6人代表队并进行备战训练.
(1)经过备战训练,从6人中随机选出2人进行成果检验,求选出的2人中至少有1个女运动员的概率;
(2)检验结束后,甲、乙两名运动员的成绩如下:
甲: ,
, ,
, ,
, ,
,
乙: ,
, ,
, ,
, ,
,
根据两组数据完成图示的茎叶图,并通过计算说明哪位运动员的成绩更稳定.
对某班学生一次英语测试的成绩分析,各分数段的分布如下图(分数取整数),由此,估计这次测验的优秀率(不小于80分)为( )

| A.92% | B.24% | C.56% | D.76% |
将某选手的9个得分去掉1个最高分,去掉1个最低分,7个剩余分数的平均分为91,现场做的9个分数的茎叶图后来有一个数据模糊,无法辨认,在图中以x表示:则7个剩余分数的方差为( )

A. |
B. |
C.36 | D. |
某班级有 名学生,其中有
名学生,其中有 名男生和
名男生和 名女生,随机询问了该班五名男生和五名女生在某次数学测验中的成绩(满分为
名女生,随机询问了该班五名男生和五名女生在某次数学测验中的成绩(满分为 分),五名男生的成绩分别为
分),五名男生的成绩分别为 ,
, ,
, ,
, ,
, ,五名女生的成绩分别为
,五名女生的成绩分别为 ,
, ,
, ,
, ,
, ,下列说法一定正确的是( )
,下列说法一定正确的是( )
| A.这种抽样方法是一种分层抽样 |
| B.这种抽样方法是一种系统抽样 |
| C.该班级男生成绩的平均数小于该班女生成绩的平均数 |
| D.这五名男生成绩的方差大于这五名女生成绩的方差 |
 是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如图是根据哈尔滨三中学生社团某日早6点至晚9点在南岗、群力两个校区附近的
是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如图是根据哈尔滨三中学生社团某日早6点至晚9点在南岗、群力两个校区附近的 监测点统计的数据(单位:毫克/立方米)列出的茎叶图,南岗、群力两个校区浓度的方差较小的是( )
监测点统计的数据(单位:毫克/立方米)列出的茎叶图,南岗、群力两个校区浓度的方差较小的是( )
| 南岗校区 |
|
群力校区 |
| 2 |
0.04 |
1 2 3 6 |
| 9 3 |
0.05 |
9 |
| 6 2 1 |
0.06 |
2 9 |
| 3 3 1 |
0.07 |
9 |
| 6 4 |
0.08 |
7 |
| 7 |
0.09 |
2 4 6 |
A.南岗校区
B.群力校区
C.南岗、群力两个校区相等
D.无法确定
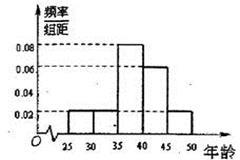
为了“城市品位、方便出行、促进发展”,南昌市拟修建穿江隧道,市某部门问卷调查了n个市民,其中赞成修建穿江隧道的市民占80%,在赞成修建穿江隧道的市民中又按年龄分组,得样本频率分布直方图如图,其中年龄在[20,30)岁的有400人,[40,50)岁的有m人,则n= ,m= .

在某次测量中得到的 样本数据如下:
样本数据如下:
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, .
.
若 样本数据恰好是
样本数据恰好是 样本数据都加
样本数据都加 后所得数据,则
后所得数据,则 ,
, 两样本的下列数字特征对应相同的是( )
两样本的下列数字特征对应相同的是( )
| A.众数 | B.平均数 | C.中位数 | D.标准差 |
某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组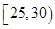 ,第2组
,第2组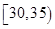 ,第3组
,第3组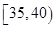 ,第4组
,第4组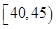 ,第5组
,第5组 ,得到的频率分布直方图如图所示。现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,年龄在第3组的人数是 ;
,得到的频率分布直方图如图所示。现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,年龄在第3组的人数是 ;
下图是2014年抚顺市举办“我看抚顺改革开放三十年”演讲比赛大赛上,七位评委为某位选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )

| A.5;1.6 | B.85;1.6 | C.85;0.4 | D.5;0.4 |
(本小题满分14分)下面的茎叶图记录了甲、乙两代表队各10名同学在一次英语听力比赛中的成绩(单位:分).已知甲代表队数据的中位数为76,乙代表队数据的平均数是75.
(1)求 ,
, 的值;
的值;
(2)若分别从甲、乙两队随机各抽取1名成绩不低于80分的学生,求抽到的学生中,甲队学生成绩不低于乙队学生成绩的概率;
(3)判断甲、乙两队谁的成绩更稳定,并说明理由(方差较小者稳定).
某单位有青年职工、中年职工、老年职工共900人,其中青年职工450人,为迅速了解职工的家庭状况,采用分层抽样的方法从中抽取样本,若样本中的青年职工为15人,则抽取的样本容量为 .
试题篮
()