如图,在正方体ABCD﹣A1B1C1D1中,AA1=2,E为AA1的中点,O是BD1的中点.
(Ⅰ)求证:平面A1BD1⊥平面ABB1A1;
(Ⅱ)求证:EO∥平面ABCD.
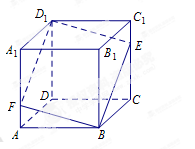
如图,四边形ABEF是等腰梯形,AB∥EF,AF=BE=2,EF=4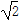 ,AB=2
,AB=2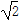 ,ABCD是矩形.AD⊥平面ABEF,其中Q,M分别是AC,EF的中点,P是BM中点.
,ABCD是矩形.AD⊥平面ABEF,其中Q,M分别是AC,EF的中点,P是BM中点.
(1)求证:PQ∥平面BCE;
(2)求证:AM⊥平面BCM;
(3)求点F到平面BCE的距离.
如图所示,在正方体 中,点
中,点 是棱
是棱 上的一个动点,平面
上的一个动点,平面 交棱
交棱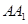 于点
于点 .则下列命题中真命题的个数是( )
.则下列命题中真命题的个数是( )
①存在点 ,使得
,使得 //平面
//平面
②存在点 ,使得
,使得 平面
平面
③对于任意的点 ,平面
,平面 平面
平面
④对于任意的点 ,四棱锥
,四棱锥 的体积均不变
的体积均不变
| A.0个 |
| B.1个 |
| C.2个 |
| D.3个 |
已知命题p:m,n为直线,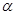 为平面,若m∥n,
为平面,若m∥n,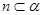 ,则m∥
,则m∥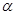 ;命题q:若a>b,则ac>bc,则下列命题为真命题的是( )
;命题q:若a>b,则ac>bc,则下列命题为真命题的是( )
A.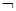 p或q p或q |
B.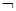 p且q p且q |
C.p或q | D.p且q |
如图,A,B,C,D四点在同一圆上,AD的延长线与BC的延长线交于E点,且 .
.
(1)证明: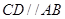 ;
;
(2)延长CD到F,延长DC到G,使得 ,证明:A,B,G,F四点共圆.
,证明:A,B,G,F四点共圆.
如图,直三棱柱ABC﹣A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.
(Ⅰ)求证:MN∥平面ABB1A1;
(Ⅱ)线段CC1上是否存在点Q,使A1B⊥平面MNQ?说明理由.
如图,在四棱锥P-ABCD 中,AB∥CD ,AB⊥AD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD,E和F分别为CD和PC的中点.求证:
(1)BE∥平面PAD;
(2)平面BEF⊥平面PCD.
若P两条异面直线l,m外的任意一点,则( )
| A.过点P有且仅有一条直线与l,m都平行 |
| B.过点P有且仅有一条直线与l,m都垂直 |
| C.过点P有且仅有一条直线与l,m都相交 |
| D.过点P有且仅有一条直线与l,m都异面 |
试题篮
()