高中数学平行线法解答题

求证：空间四边形相邻两边中点的连线平行于经过另外两边所在的平面．
已知：如图，空间四边形中，，分别是，的中点．
求证：

如图2-5,S是正方形ABCD所在平面外一点,且SA=SB=SC=SD,点P在SC上,满足SP∶PC=1∶2,又点M与N分别在SB和SD上,且BM=DN,求当MN∶BD的值为多少时,SA∥平面PMN？

图2-5

已知：如图，为异面直线的公垂线，平面，平面，
．求证：．

 

如图，是平行四边形，点是平面外一点，是的中点，在上取一点，过和作平面交平面于．
求证：．

 

已知空间四边形，，分别是△和△的重心．
求证：平面．

已知空间四点不在同一平面内，求证：既不平行也不相交．

如图，在空间四边形中，分别是的中点．
求证：（1）平面；（2）平面．

 

如图，在四棱锥的底面边长和各侧棱长都是13，分别是上的点且．求证：直线平面

 

正方体ABCD—A₁B₁C₁D₁中，E、F、G分别是棱DA、DC、DD₁的中点，试找出过正方体的三个顶点且与平面EFG平行的平面，并证明.

如图,已知三棱锥P-ABC中，PA、PB、PC与底面ABC成相等的角，∠CAB=90°,AC=AB,D为BC的中点，E点在PB上，PC∥截面EAD.

(1)求证:平面PBC⊥底面ABC.
(2)若AB=PB，求AE与底面ABC所成角的正弦值.

已知ABCD是梯形，AD∥BC，P是平面ABCD外一点,
BC=2AD,点E在棱PA上，且PE=2EA.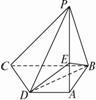

求证：PC∥平面EBD.

如图所示，在正方体ABCD-A₁B₁C₁D₁中，M、N分别是C₁C、B₁C₁的中点.
求证：MN∥平面A₁BD.

如图所示，在平行六面体ABCD—A₁B₁C₁D₁中，O是B₁D₁的中点，
求证：B₁C∥平面ODC₁.

如图所示，正四棱锥P—ABCD的各棱长均为13，M，N分别为PA，BD上的点，且PM∶MA=BN∶ND=5∶8.

（1）求证：直线MN∥平面PBC；
（2）求线段MN的长.

正方形ABCD与正方形ABEF所在平面相交于AB，在AE、BD上各有一点P、Q，且AP=DQ.求证：PQ∥平面BCE.