某重点高校数学教育专业的三位毕业生甲、乙、丙参加了一所中学的招聘面试,
面试合格者可以正式签约,毕业生甲表示只要面试合格就签约,毕业生乙和丙则约定:两人
面试都合格就一同签约,否则两人都不签约,设每人面试合格的概率都是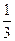 ,且面试是否合
,且面试是否合
格互不影响,求:(I)至少有1人面试合格的概率;(II)签约人数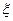 的分布列和数学期望。
的分布列和数学期望。
某足球俱乐部2013年10月份安排4次体能测试,规定:按顺序测试,一旦测试合格就不必参加以后的测试,否则4次测试都要参加。若运动员小李4次测试每次合格的概率组成一个公差为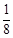 的等差数列,他第一次测试合格的概率不超过
的等差数列,他第一次测试合格的概率不超过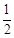 ,且他直到第二次测试才合格的概率为
,且他直到第二次测试才合格的概率为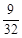 。
。
(Ⅰ)求小李第一次参加测试就合格的概率P1;
(2)求小李10月份参加测试的次数x的分布列和数学期望。
假设每一架飞机的引擎在飞行中出现故障的概率为1-P,且各引擎是否出故障是独立的,已知4引擎飞机中至少有3个引擎正常运行,飞机就能成功运行;2引擎飞机中要2个引擎全部正常运行,飞机才能成功运行.要使4引擎飞机比2引擎飞机更安全,则P的取值范围?
甲、乙两人进行乒乓球比赛,比赛规则为“3局2胜”,即以先赢2局者为胜.根据经验,每局比赛中甲获胜的概率为0.6,则本次比赛中甲以2:1的比分获胜的概率为( )
| A.0.288 | B.0.144 | C.0.432 | D.0.648 |
设随机变量X的分布列为P(X=k)=pk(1-p)1-k(k=0.1,0<p<1),则E(X)=________.
(本小题满分12分)抛一枚均匀的骰子(骰子的六面分别有数字1、2、3、4、5、6)来构造数列
(1)求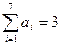 的概率;(2)若
的概率;(2)若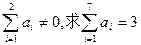 的概率.
的概率.
在2008年北京奥运会羽毛球女单决赛中,中国运动员张宁以2:1力克排名世界第一的队友谢杏芳,蝉联奥运会女单冠军.羽毛球比赛按“三局二胜制”的规则进行(即先胜两局的选手获胜,比赛结束),且各局之间互不影响.根据两人以往的交战成绩分析,谢杏芳在前两局的比赛中每局获胜的概率是0.6,但张宁在前二局战成1:1的情况下,在第三局中凭借过硬的心理素质,获胜的概率为0.6.若张宁与谢杏芳下次在比赛上相遇.
(1)求张宁以2:1获胜的概率;
(2)求张宁失利的概率.
实验女排和育才女排两队进行比赛,在一局比赛中实验女排获胜的概率是2/3,没有平局.若采用三局两胜制,即先胜两局者获胜且比赛结束,则实验女排获胜的概率等于
A. |
B. |
C. |
D. |
某射手射击1次,击中目标的概率是0.9,他连续射击4次,且各次射击是否击中目标相互之间没有影响,有下列结论:①他第3次击中目标的概率是0.9;②他恰好击中目标3次的概率是0.93×0.1;③他至少击中目标1次的概率是1-0.14.其中结论正确的是________.(写出所有正确结论的序号)
如图;现有一迷失方向的小青蛙在3处,它每跳动一次可以等机会地进入相邻的任意一格(如若它在5处,跳动一次,只能进入3处,若在3处,则跳动一次可以等机会进入l,2,4,5处),则它在第三次跳动后,进入5处的概率是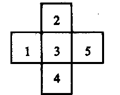
A.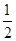 |
B.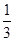 |
C.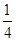 |
D.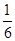 |
试题篮
()