高中数学正交试验设计方法解答题

高三年级有3名男生和1名女生为了报某所大学，事先进行了多方详细咨询，并根据自己的高考成绩情况，最终估计这3名男生报此所大学的概率都是，这1名女生报此所大学的概率是．且这4人报此所大学互不影响。
（Ⅰ）求上述4名学生中报这所大学的人数中男生和女生人数相等的概率；
（Ⅱ）在报考某所大学的上述4名学生中，记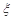为报这所大学的男生和女生人数的和，试求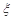的分布列和数学期望．

为了防止受到核污染的产品影响我国民众的身体健康，要求产品进入市场前必须进行两轮核放射检测，只有两轮都合格才能进行销售。已知某产品第一轮检测不合格的概率为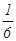，第二轮检测不合格的概率为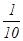，两轮检测是否合格相互没有影响。
（1）求该产品不能销售的概率
（2）如果产品可以销售，则每件产品可获利40元；如果产品不能销售，则每件产品亏损80元（即获利-80元）。已知一箱中有4件产品，记可销售的产品数为X，求X的分布列，并求一箱产品获利的均值。

）已知某音响设备由五个部件组成，A电视机，B影碟机，C线路，D左声道和E右声道，其中每个部件工作的概率如图所示，能听到声音，当且仅当A与B中有一个工作，C工作，D与E中有一个工作；且若D和E同时工作则有立体声效果.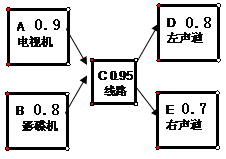

（1）求能听到立体声效果的概率；
（2）求听不到声音的概率.（结果精确到0.01）

某医院将一专家门诊已诊的1000例病人的病情及诊断所用时间（单位：分钟）进行了统计，如下表．若视频率为概率，请用有关知识解决下列问题．

病症及代号	普通病症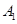	复诊病症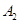	常见病症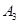	疑难病症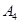	特殊病症
人数	100	300	200	300	100
每人就诊时间（单位：分钟）	3	4	5	6	7

用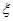表示某病人诊断所需时间，求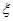的数学期望．
并以此估计专家一上午（按3小时计算）可诊断多少病人；
某病人按序号排在第三号就诊，设他等待的时间为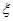，求；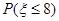
求专家诊断完三个病人恰好用了一刻钟的概率．

有甲，乙两个盒子，甲盒中装有2个小球，乙盒中装有3个小球，每次随机选取一个盒子并从中取出一个小球
（1）当甲盒中的球被取完时，求乙盒中恰剩下1个球的概率；
（2）当第一次取完一个盒子中的球时，另一个盒子恰剩下个球，求的分布列及期望。

某足球俱乐部2013年10月份安排4次体能测试，规定：按顺序测试，一旦测试合格就不必参加以后的测试，否则4次测试都要参加。若运动员小李4次测试每次合格的概率组成一个公差为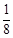的等差数列，他第一次测试合格的概率不超过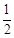，且他直到第二次测试才合格的概率为。
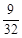（Ⅰ）求小李第一次参加测试就合格的概率P₁；
（2）求小李10月份参加测试的次数x的分布列和数学期望。

某射手击中目标的概率为0.8，每次射击的结果相互独立，现射击10次，问他最有可能射中几次？

为了解某市市民对政府出台楼市限购令的态度，在该市随机抽取了50名市民进行调查，他们月收入（单位：百元）的频数分布及对楼市限购令的赞成人数如下表：

月收入		[25，35）	[35，45）
频数	5	10	15	10	5	5
赞成人数	4	8	8	5	2	1

将月收入不低于55的人群称为“高收入族”，月收入低于55的人群称为“非高收人族”。
（Ⅰ）根据已知条件完成下面的2×2列联表，有多大的把握认为赞不赞成楼市限购令与收入高低有关？
已知：，
当<2.706时，没有充分的证据判定赞不赞成楼市限购令与收入高低有关；
当>2.706时，有90％的把握判定赞不赞成楼市限购令与收入高低有关；
当>3.841时，有95％的把握判定赞不赞成楼市限购令与收入高低有关；
当>6.635时，有99％的把握判定赞不赞成楼市限购令与收入高低有关。

	非高收入族	高收入族	总计
赞成
不赞成
总计

（Ⅱ）现从月收入在[55，65）的人群中随机抽取两人，求所抽取的两人中至少一人赞成楼市限购令的概率。

已知射手甲射击一次，命中9环（含9环）以上的概率为0.56，命中8环的概率为0.22，命中7环的概率为0.12．
①求甲射击一次，命中不足8环的概率.
②求甲射击一次，至少命中7环的概率.

甲、乙两人各进行3次射击，甲每次击中目标的概率为，乙每次击中目标的概率为
求：（1）乙至少击中目标2次的概率；
（2）乙恰好比甲多击中目标2次的概率

甲、乙、丙三人进行乒乓球练习赛，其中两人比赛，另一人当裁判，每局比赛结束时，负的一方在下一局当裁判．设各局中双方获胜的概率均为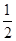，各局比赛的结果相互独立，第1局甲当裁判．
（1）求第4局甲当裁判的概率；
（2）用X表示前4局中乙当裁判的次数，求X的分布列和数学期望．

5名工人独立地工作，假定每名工人在1小时内平均12分钟需要电力（即任一时刻需要电力的概率为12/60）
（1）设X为某一时刻需要电力的工人数，求 X的分布列及期望；
（2）如果同一时刻最多能提供3名工人需要的电力，求电力超负荷的概率，并解释实际意义．

某中学经市批准建设分校，工程从2010年底开工到2013年底完工，分三期完成，经过初步招标淘汰后，确定由甲、乙两建筑公司承建，且每期工程由两公司之一独立完成，必须在建完前一期工程后再建后一期工程，已知甲公司获得第一期，第二期，第三期工程承包权的概率分别是，，．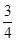
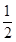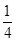(I)求甲乙两公司均至少获得l期工程的概率；
(II)求甲公司获得的工程期数的分布列和数学期望E(X)．

甲与乙两人掷硬币，甲用一枚硬币掷3次，记正面朝上的次数为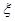；乙用这枚硬币掷2次，记正面朝上的次数为。
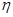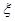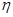（1）分别求与的期望；
（2）规定：若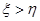，则甲获胜；若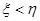，则乙获胜，分别求出甲和乙获胜的概率.

(8分)一个口袋有5个同样大小的球，编号为1、2、3、4、5，从中同时取出3个，以ξ表示取出球编号的最小号码，求(1)ξ的分布列．(2)取出球编号最小的号码小于等于2的概率