高中数学正交试验设计方法解答题

在人群流量较大的街道，有一中年人吆喝“送钱”，只见他手拿一黑色小布袋，袋中有3只黄色、3只白色的乒乓球（其体积、质地完成相同），旁边立着一块小黑板写道：
摸球方法：从袋中随机摸出3个球，若摸得同一颜色的3个球，摊主送给摸球者5元钱；若摸得非同一颜色的3个球，摸球者付给摊主1元钱.
（Ⅰ）摸出的3个球为白球的概率是多少？  
（Ⅱ）摸出的3个球为2个黄球1个白球的概率是多少？
（III）假定一天中有100人次摸奖，试从概率的角度估算一下这个摊主一个月（按30天计）能赚多少钱？

某饮料公司招聘了一名员工，现对其进行一项测试，以便确定工资级别.公司准备了两种不同的饮料共8杯，其颜色完全相同，并且其中4杯为饮料，另外4杯为饮料.公司要求此员工一一品尝后，从8杯饮料中选出4杯饮料.若4杯都选对，则月工资定为3500元；若4杯选对3杯，则月工资定为2800元；否则月工资定为2100元.令表示此人选对饮料的杯数.假设此人对和两种饮料没有鉴别能力.
（1）求的分布列；
（2）求此员工月工资被定为2100元的概率.

2011年4月28日世界园艺博览会将在陕西西安浐灞生态区举行，为了接待来自国内外的各界人士，需招募一批志愿者，要求志愿者不仅要有一定的气质，还需有丰富的人文、地理、历史等文化知识。志愿者的选拔分面试和知识问答两场，先是面试，面试通过后每人积60分，然后进入知识问答。知识问答有A,B,C,D四个题目，答题者必须按A,B,C,D顺序依次进行，答对A,B,C,D四题分别得20分、20分、40分、60分，每答错一道题扣20分，总得分在面试60分的基础上加或减。答题时每人总分达到100分或100分以上，直接录用不再继续答题；当四道题答完总分不足100分时不予录用。
假设志愿者甲面试已通过且第二轮对A,B,C,D四个题回答正确的概率依次是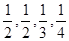，且各题回答正确与否相互之间没有影响.
(Ⅰ) 用X表示志愿者甲在知识问答结束时答题的个数，求X的分布列和数学期望；
（Ⅱ）求志愿者甲能被录用的概率.

某次乒乓球比赛的决赛在甲乙两名选手之间举行，比赛采用五局三胜制，决出胜负即停止比赛。按以往的比赛经验，每局比赛中，甲胜乙的概率为。
（1）求比赛三局甲获胜的概率；
（2）求甲获胜的概率；
（3）设比赛的局数为X，求X的分布列和数学期望。

(8分)在5道题中有3道理科题和2道文科题，如果不放回地依次抽取2道题，求;
(1) 第1次和第2次抽都到理科题的概率;
(2)在第1次抽到理科题的条件下, 第2次抽到理科题的概率;

将一个半径适当的小球放入如图所示的容器最上方的入口处，小球将自由下落．小球在
下落的过程中，将3次遇到黑色障碍物，最后落入袋或袋中．已知小球每次遇到黑色障碍物时，向左、右两边下落的概率都是．
（Ⅰ）求小球落入袋中的概率；
（Ⅱ）在容器入口处依次放入4个小球，记为落入袋中的小球个数，试求的概率和的数学期望．

(10分)某运动员射击一次所得环数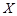的分布如下：

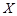	0~6	7	8	9	10
	0

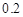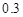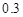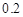现进行两次射击，以该运动员两次射击中最高环数作为他的成绩，记为.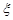
(I)求该运动员两次都命中7环的概率
(II)求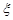的分布列
(III)求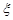的数学期望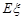

甲、乙两队在进行一场五局三胜制的排球比赛中，规定先赢三局的队获胜，并且比赛就此结束，现已知甲、乙两队每比赛一局，甲队获胜的概率为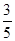，乙队获胜的概率为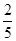，且每局比赛的胜负是相互独立的，问：
（1）甲队以获胜的概率是多少？
（2）乙队获胜的概率是多少？

(10分) 甲、乙两人参加一次英语口语考试，已知在备选的10道试题中，甲能答对其中的6题，乙能答对其中的8题．规定每次考试都从备选题中随机抽出3题进行测试，至少答对2题才算合格．
(1)分别求甲、乙两人考试合格的概率；
(2)求甲、乙两人至少有一人考试合格的概率．

袋子里有大小相同但标有不同号码的3个红球和4个黑球，从袋子里随机取出4个球.
⑴求取出的红球数的概率分布列；
⑵若取到每个红球得2分，取到每个黑球得1分，求得分不超过5分的概率.

某中学将100名高一新生分成水平相同的甲、乙两个“平行班”，每班50人．陈老师采用A、B两种不同的教学方式分别在甲、乙两个班级进行教改实验．为了了解教学效果，期末考试后，陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计，作出茎叶图如下．记成绩不低于90分者为“成绩优秀”．

甲		乙
6	9	3 6 7 9 9
9 5 1 0	8	0 1 5 6
9 9 4 4 2	7	3 4 5 8 8 8
8 8 5 1 1 0	6	0 7 7
4 3 3 2	5	2 5

 
(1)在乙班样本中的20个个体中，从不低于86分的成绩中随机抽取2个，求抽出的两个均“成绩优秀”的概率；
(2)由以上统计数据填写下面列联表，并判断是否有90%的把握认为：“成绩优秀”与教学方式有关.

	甲班(A方式)	乙班(B方式)	总计
成绩优秀
成绩不优秀
总计

 
附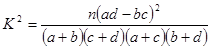：,其中n＝a＋b＋c＋d.)

P(K^2≥k)	0.25	0.15	0.10	0.05	0.025	0.01	0.005	0.001
k	1.323	2.072	2.706	3.841	5.024	6.635	7.879	10.828

 

根据以往的经验，某工程施工期间的降水量 $X$（单位： $mm$）对工期的影响如下表：

降水量 $X$	$X<300$	$300\le X<700$	$700\le X<900$	$X\ge 900$
工期延误天数 $Y$	0	2	6	10

历年气象资料表明，该工程施工期间降水量 $X$小于300，700，900的概率分别为0.3，0.7，0.9. 求：
（Ⅰ）工期延误天数 $Y$的均值与方差；
（Ⅱ）在降水量X至少是300的条件下，工期延误不超过6天的概率.

某种产品按质量标准分成五个等级，等级编号依次为1,2,3,4,5．现从一批产品中随机抽取20件，对其等级编号进行统计分析，得到频率分布表如下：

等级	1	2	3	4	5
频率	a	0．2	0．45	b	c

（1）若所抽取的20件产品中，等级编号为4的恰有3件，等级编号为5的恰有2件，求a，b，c的值；
（2）在（1）的条件下，将等级编号为4的3件产品记为x_l，x₂，x₃，等级编号为5的2件产品记为y_l ,y₂，现从x_l，x₂，x₃，y_l,y₂这5件产品中任取两件（假定每件产品被取出的可能性相同），写出所有可能的结果，并求这两件品的级编号恰好相同的概率。

甲、乙、丙3人投篮,投进的概率分别是,  ,  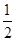．(Ⅰ)现3人各投篮1次,求3人都没有投进的概率;(Ⅱ)用ξ表示乙投篮3次的进球数,求随机变量ξ的概率分布及数学期望Eξ

(本题满分12分)有朋自远方来，他乘火车、轮船、汽车、飞机来的概率分别为0.3,0.2,0.1,0.4.
试问：(1)他乘火车或乘飞机来的概率；
(2)他不乘轮船来的概率；
(3)如果他来的概率为0.5，请问他有可能是乘何种交通工具来的．
即他不乘轮船来的概率为0.8.