高中数学正交试验设计方法解答题

（本小题满分12分）
将10个白小球中的3个染成红色，3个染成黄色，试解决下列问题：
求取出3个小球中红球个数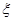的分布列和数学期望；
求取出3个小球中红球个数多于白球个数的概率.

某市为了了解今年高中毕业生的体能状况，从本市某校高中毕业班中抽取一个班进行铅球测试，成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后，分成6组画出频率分布直方图的一部分(如图)，已知从左到右前5个小组的频率分别为0.04，0.10，0.14，0.28，0.30.第6小组的频数是7.
( I ) 求这次铅球测试成绩合格的人数；
(II)用此次测试结果估计全市毕业生的情况.若从今年的高中毕业生中随机抽取两名，记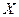表示两人中成绩不合格的人数，求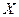的数学期望和方差.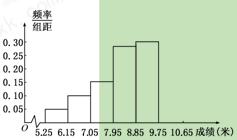

（本小题满分12分）为预防H₁N₁病毒爆发，某生物技术公司研制出一种新流感
疫苗，为测试该疫苗的有效性（若疫苗有效的概率小于90%，则认为测试没有通过），公司
选定2000个流感样本分成三组，测试结果如下表：

分组	A组	B组	C组
疫苗有效	673
疫苗无效	77	90

已知在全体样本中随机抽取1个，抽到B组疫苗有效的概率是0.33．
（I）现用分层抽样的方法在全体样本中抽取360个测试结果，问应在C组抽取样本多少个？
（II）已知，，求通过测试的概率．

（本小题满分12分）
袋中有4个黑球、3个白球、2个红球，从中任取2个球，每取到一个黑球记0分，每取到一个白球记1分，每取到一个红球记2分，用X表示得分数．
（1）求X的概率分布列；
（2）求X的数学期望EX．

从某批产品中，有放回地抽取产品2次，每次随机抽取1件，假设事件A：“取出的2件产品中至多有1件是二等品”的概率为0.84．
（Ⅰ）求事件“从该批产品中任取1件产品，取到的是二等品”的概率p；
（Ⅱ）若从20件该产品中任意抽取3件，求事件B：“取出的3件产品中至少有一件二等品”的概率．

在一个有奖问答的电视节目中，参赛选手顺序回答三个问题，答对各个问题所获奖金（单位：元）对应如下表：

当一个问题回答正确后，选手可选择继续回答下一个问题，也可选择放弃．若选择放弃，选手将获得答对问题的累计奖金，答题结束；若有任何一个问题回答错误，则全部奖金归零，答题结束．设一名选手能正确回答的概率分别为，正确回答一个问题后，选择继续回答下一个问题的概率均为，且各个问题回答正确与否互不影响．
（Ⅰ）按照答题规则，求该选手回答正确但所得奖金为零的概率；
（Ⅱ）设该选手所获奖金总数为，求的分布列与数学期望．

甲乙两人各有相同的小球10个，在每人的10个小球中都有5个标有数字1，3个标有数字2，2个标有数字3。两人同时分别从自己的小球中任意抽取1个，规定：若抽取的两个小球上的数字相同，则甲获胜，否则乙获胜，求乙获胜的概率。

某陶瓷厂准备烧制甲、乙、丙三件不同的工艺品，制作过程必须先后经过两次烧制，当第一次烧制合格后方可进行第二次烧制，两次烧制过程相互独立．根据该厂现有的技术水平，经过第一次烧制后，甲、乙、丙三件产品的合格率依次为，，．经过第二次烧制后，甲、乙、丙三件产品的合格率均为．
(Ⅰ)求第一次烧制后恰有一件产品合格的概率；
(Ⅱ)求经过前后两次烧制后三件产品均合格的概率．

一个袋中有1个白球和4个黑球，每次从中任取一个球，每次所取的球放回，直到取得白球为止，但摸球次数不超过5次，求取球次数的分布列

某装置由两套系统M,N组成，只要有一套系统工作正常，该装置就可以正常工作。每套系统都由三种电子模块T1,T2,T3组成（如图所示已知T1,T2,T3正常工作的概率都是，且T1,T2,T3能否正常工作相互独立.(注：对每一套系统或每一种电子模块而言,只要有电流通过就能正常工作.)

(I )分别求系统M,N正常工作的概率；
(II)设该装I中两套系统正常工作的套数为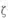，求的分布列和期望.

现有三种基本电子模块，电流能通过的概率都是P，电流能否通过各模块相互独立.已知中至少有一个能通过电流的概率为0.999.现由该电子模块组装成某预警系统M(如图所示），针对系统M而言，只要有电流通过该系统就能正常工作.

(1)求P值
(II)求预警系统M正常工作的概率

（本小题满分12分）
已知射手甲射击一次，击中目标的概率是．
（1）求甲射击5次，恰有3次击中目标的概率；
（2）假设甲连续2次未击中目标，则停止其射击，求甲恰好射击5次后，被停止射击的概率．

（本题12分）已知某种从太空带回的植物种子每粒成功发芽的概率都为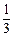，某植物研究所分两个小组分别独立开展该种子的发芽实验，每次实验种一粒种子，假定某次实验种子发芽则称该次实验是成功的，如果种子没有发芽，则称该次实验是失败的．
(1) 第一小组做了三次实验，求实验成功的平均次数；
(2) 第二小组连续进行实验，求实验首次成功时所需的实验次数的期望；
(3)两个小组分别进行2次试验，求至少有2次实验成功的概率．

（本小题满分12 分）
从甲地到乙地一天共有A、B 两班车，由于雨雪天气的影响，一段时间内A 班车正点到达乙地的概率为0．7，B 班车正点到达乙地的概率为0．75。
（1）有三位游客分别乘坐三天的A 班车，从甲地到乙地，求其中恰有两名游客正点到达的概率（答案用数字表示）。
（2）有两位游客分别乘坐A、B 班车，从甲地到乙地，求其中至少有1 人正点到达的概率（答案用数字表示）。

如果在一次试验中，某事件A发生的概率为p，那么在n次独立重复试验中，求事件A发生偶数次的概率．