高中数学正交试验设计方法解答题

甲、乙、丙3人投篮,投进的概率分别是,  ,  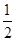．(Ⅰ)现3人各投篮1次,求3人都没有投进的概率;(Ⅱ)用ξ表示乙投篮3次的进球数,求随机变量ξ的概率分布及数学期望Eξ

（本小题满分12 分）
从甲地到乙地一天共有A、B 两班车，由于雨雪天气的影响，一段时间内A 班车正点到达乙地的概率为0．7，B 班车正点到达乙地的概率为0．75。
（1）有三位游客分别乘坐三天的A 班车，从甲地到乙地，求其中恰有两名游客正点到达的概率（答案用数字表示）。
（2）有两位游客分别乘坐A、B 班车，从甲地到乙地，求其中至少有1 人正点到达的概率（答案用数字表示）。

某种产品按质量标准分成五个等级，等级编号依次为1,2,3,4,5．现从一批产品中随机抽取20件，对其等级编号进行统计分析，得到频率分布表如下：

等级	1	2	3	4	5
频率	a	0．2	0．45	b	c

（1）若所抽取的20件产品中，等级编号为4的恰有3件，等级编号为5的恰有2件，求a，b，c的值；
（2）在（1）的条件下，将等级编号为4的3件产品记为x_l，x₂，x₃，等级编号为5的2件产品记为y_l ,y₂，现从x_l，x₂，x₃，y_l,y₂这5件产品中任取两件（假定每件产品被取出的可能性相同），写出所有可能的结果，并求这两件品的级编号恰好相同的概率。

某人对一目标进行射击，每次命中率都是0.25，若使至少命中1次的概率不小于0.75，至少应射击几次？

（本小题共13分）某市医疗保险实行定点医疗制度，按照“就近就医、方便管理”的原则，参加保险人员可自主选择四家医疗保险定点医院和一家社区医院作为本人就诊的医疗机构．若甲、乙、丙、丁4名参加保险人员所在地区附近有A，B，C三家社区医院，并且他们的选择是相互独立的．
（Ⅰ）求甲、乙两人都选择A社区医院的概率；
（Ⅱ）求甲、乙两人不选择同一家社区医院的概率；
（Ⅲ）设4名参加保险人员中选择A社区医院的人数为ξ，求ξ的分布列和数学期望．

在某校举办的元旦有奖知识问答中，甲、乙、丙三人同时回答一道有关环保知识的问题，已知甲回答对这道题的概率是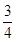，甲、丙两人都回答错的概率是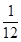，乙、丙两人都回答对的概率是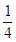.(Ⅰ)求乙、丙两人各自回答对这道题的概率；(Ⅱ)用表示回答对该题的人数，求的分布列和数学期望E.

甲、乙两队在进行一场五局三胜制的排球比赛中，规定先赢三局的队获胜，并且比赛就此结束，现已知甲、乙两队每比赛一局，甲队获胜的概率为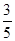，乙队获胜的概率为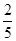，且每局比赛的胜负是相互独立的，问：
（1）甲队以获胜的概率是多少？
（2）乙队获胜的概率是多少？

(本题满分12分)某电视生产厂家今年推出A、B、C、D四种款式电视机，每种款式电视机的外观均有黑色、银白色两种。四月份的电视机产量如下表（单位：台）

	款式A	款式B	款式C	款式D
黑色	150	200	200
银白色	160	180	200	150

若按电视机的款式采取分层抽样的方法在这个月生产的电视机中抽取70台，其中有C种款式的电视机20台。
（1）  求的值；
（2）  若在C款式电视机中按颜色进行分层抽样抽取一个容量为6的样本，然后将该样本看成一个总体，从中任取2台，求恰有1台黑色、1台银白色电视的概率；
（3）  用简单随机抽样的方法从A种款式电视机中抽取10台，对其进行检测，它们的得分如下：94，92，92，96，97，95，98，90，94，97。如果把这10台电视机的得分看作一个样本，从中任取一个数，求该数与样本平均数之差的绝对值不超过2的概率。

某电视台有A、B两种智力闯关游戏，甲、乙、丙、丁四人参加，其中甲乙两人各自独立进行游戏A，丙丁两人各自独立进行游戏B.已知甲、乙两人各自闯关成功的概率均为，丙、丁两人各自闯关成功的概率均为.
(I )求游戏A被闯关成功的人数多于游戏B被闯关成功的人数的概率；
(II) 记游戏A、B被闯关成功的总人数为，求的分布列和期望.

中国黄石第三届国际矿冶文化旅游节将于2012年8月20日在黄石铁山举行，为了搞好接待工作，组委会准备在湖北理工学院和湖北师范学院分别招募8名和12名志愿者，将这20名志愿者的身高编成如下茎叶图（单位：cm）
若身高在175cm以上（包括175cm）定义为“高个子”，身高在175cm以下（不包括175cm）定义为“非高个子”，且只有湖北师范学院的“高个子”才能担任“兼职导游”。
（1）根据志愿者的身高编茎叶图指出湖北师范学院志愿者身高的中位数；
（2）如果用分层抽样的方法从“高个子”和“非高个子”中抽取5人，再从这5人中选2人，那么至少有一人是“高个子”的概率是多少？
（3）若从所有“高个子”中选3名志愿者，用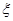表示所选志愿者中能担任“兼职导游”的人数，试写出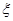的分布列，并求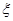的数学期望。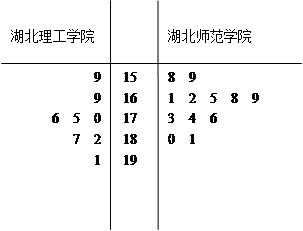

某气象站天气预报的准确率为，计算（结果保留到小数点后面第2位）
（1）5次预报中恰有2次准确的概率；
（2）5次预报中至少有2次准确的概率；
（3）5次预报中恰有2次准确，且其中第次预报准确的概率

甲投篮命中率为O．8，乙投篮命中率为0.7，每人投3次，两人恰好都命中2次的概率是多少?

（本小题满分12分）
将10个白小球中的3个染成红色，3个染成黄色，试解决下列问题：
求取出3个小球中红球个数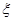的分布列和数学期望；
求取出3个小球中红球个数多于白球个数的概率.

某中学的高二(1)班男同学有名，女同学有名，老师按照分层抽样的方法组建了一个人的课外兴趣小组．
（１）求某同学被抽到的概率及课外兴趣小组中男、女同学的人数；
（２）经过一个月的学习、讨论，这个兴趣小组决定选出两名同学做某项实验，方法是先从小组里选出名同学做实验，该同学做完后，再从小组内剩下的同学中选一名同学做实验，求选出的两名同学中恰有一名女同学的概率；
（３）实验结束后，第一次做实验的同学得到的实验数据为，第二次做实验的同学得到的实验数据为，请问哪位同学的实验更稳定？并说明理由.

根据以往的经验，某工程施工期间的降水量 $X$（单位： $mm$）对工期的影响如下表：

降水量 $X$	$X<300$	$300\le X<700$	$700\le X<900$	$X\ge 900$
工期延误天数 $Y$	0	2	6	10

历年气象资料表明，该工程施工期间降水量 $X$小于300，700，900的概率分别为0.3，0.7，0.9. 求：
（Ⅰ）工期延误天数 $Y$的均值与方差；
（Ⅱ）在降水量X至少是300的条件下，工期延误不超过6天的概率.