某足球俱乐部2013年10月份安排4次体能测试,规定:按顺序测试,一旦测试合格就不必参加以后的测试,否则4次测试都要参加。若运动员小李4次测试每次合格的概率组成一个公差为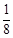 的等差数列,他第一次测试合格的概率不超过
的等差数列,他第一次测试合格的概率不超过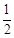 ,且他直到第二次测试才合格的概率为
,且他直到第二次测试才合格的概率为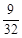 。
。
(Ⅰ)求小李第一次参加测试就合格的概率P1;
(2)求小李10月份参加测试的次数x的分布列和数学期望。
甲乙两人各有相同的小球10个,在每人的10个小球 中都有5个标有数字1,3个标有数字2,2个标有数字3。两人同时分别从自己的小球中任意抽取1个,规定:若抽取的两个小球上的数字相同,则甲获胜,否则乙获胜,求乙获胜的概率。
中都有5个标有数字1,3个标有数字2,2个标有数字3。两人同时分别从自己的小球中任意抽取1个,规定:若抽取的两个小球上的数字相同,则甲获胜,否则乙获胜,求乙获胜的概率。
为了防止受到核污染的产品影响我国民众的身体健康,要求产品进入市场前必须进行两轮核放射检测,只有两轮都合格才能进行销售。已知某产品第一轮检测不合格的概率为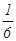 ,第二轮检测不合格的概率为
,第二轮检测不合格的概率为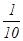 ,两轮检测是否合格相互没有影响。
,两轮检测是否合格相互没有影响。
(1)求该产品不能销售的概率
(2)如果产品可以销售,则每件产品可获利40元;如果产品不能销售,则每件产品亏损80元(即获利-80元)。已知一箱中有4件产品,记可销售的产品数为X,求X的分布列,并求一箱产品获利的均值。
某篮球队与其他6支篮球队依次进行6场比赛,每场均决出胜负,设这支篮球队与其他篮球队比赛胜场的事件是独立的,并且胜场的概率是 .
.
(1)求这支篮球队首次胜场前已经负了两场的概率;
(2)求这支篮球队在6场比赛中恰好胜了3场的概率;
(3)求这支篮球队在6场比赛中胜场数的期望和方差.
成都市为“市中学生知识竞赛”进行选拔性测试,且规定:成绩大于或等于90分的有参赛资格,90分以下(不包括90分)的则被淘汰。若现有500人参加测试,学生成绩的频率分布直方图如下: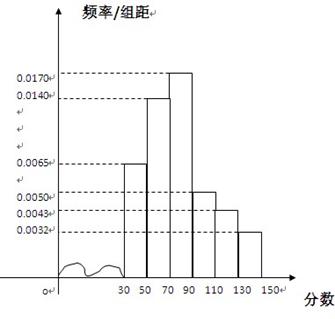
(I)求获得参赛资格的人数;
(II)根据频率直方图,估算这500名学生测试的平均成绩;
(III)若知识竞赛分初赛和复赛,在初赛中每人最多有3次选题答题的机会,累计答对2题或答错2题即终止,答对2题者方可参加复赛,已知参赛者甲答对每一个问题的概率都相同,并且相互之间没有影响,已知他连续两次答错的概率为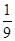 ,求甲通过初赛的概率.
,求甲通过初赛的概率.
若盒中装有同一型号的灯泡共 只,其中有
只,其中有 只合格品,
只合格品, 只次品。
只次品。
(1) 某工人师傅有放回地连续从该盒中取灯泡 次,每次取一只灯泡,求
次,每次取一只灯泡,求 次取到次品的概率;
次取到次品的概率;
(2) 某工人师傅用该盒中的灯泡去更换会议室的一只已坏灯泡,每次从中取一灯泡,若是正品则用它更换已坏灯泡,若是次品则将其报废(不再放回原盒中),求成功更换会议室的已坏灯泡所用灯泡只数 的分布列和数学期望.
的分布列和数学期望.
为了解七班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
| |
喜爱打篮球 |
不喜爱打篮球 |
合计 |
| 男生 |
|
5 |
|
| 女生 |
10 |
|
|
| 合计 |
|
|
50 |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为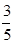 .
.
(1)请将上面的列联表补充完整(不用写计算过程);
(2)能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关?说明你的理由;
(3)现从女生中抽取2人进一步调查,设其中喜爱打篮球的女生人数为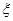 ,求
,求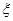 的分布列与期望.
的分布列与期望.
下面的临界值表供参考:
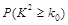 |
0.15 |
0.10 |
0.05[ |
0.025 |
0.010 |
0.005 |
0.001 |
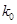 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: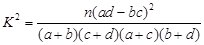 ,其中
,其中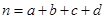 )
)
设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别是0.6,0.5,0.5,0.4,各人是否使用设备相互独立,
(1)求同一工作日至少3人需使用设备的概率;
(2)实验室计划购买台设备供甲、乙、丙、丁使用,若要求"同一工作日需使用设备的人数大于
的概率小于0.1,求
的最小值.
我校社团联即将举行一届象棋比赛,规则如下:两名选手比赛时,每局胜者得 分,负者得
分,负者得 分,比赛进行到有一人比对方多
分,比赛进行到有一人比对方多 分或打满
分或打满 局时结束.假设选手甲与选手乙比赛时,甲每局获胜的概率皆为
局时结束.假设选手甲与选手乙比赛时,甲每局获胜的概率皆为 ,且各局比赛胜负互不影响.
,且各局比赛胜负互不影响.
(Ⅰ)求比赛进行 局结束,且乙比甲多得
局结束,且乙比甲多得 分的概率;
分的概率;
(Ⅱ)设 表示比赛停止时已比赛的局数,求随机变量
表示比赛停止时已比赛的局数,求随机变量 的分布列和数学期望.
的分布列和数学期望.
为了解心肺疾病是否与年龄相关,现随机抽取了40名市民,得到数据如下表:
| |
患心肺疾病 |
不患心肺疾病 |
合计 |
| 大于40岁 |
16 |
|
|
| 小于等于40岁 |
|
12 |
|
| 合计 |
|
|
40 |
已知在全部的40人中随机抽取1人,抽到不患心肺疾病的概率为
(1)请将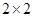 列联表补充完整;
列联表补充完整;
(2)已知大于40岁患心肺疾病市民中,经检查其中有4名重症患者,专家建议重症患者住院治疗,现从这16名患者中选出两名,记需住院治疗的人数为 ,求
,求 的分布列和数学期望;
的分布列和数学期望;
(3)能否在犯错误的概率不超过0.01的前提下认为患心肺疾病与年龄有关?
下面的临界值表供参考:
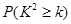 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: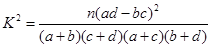 ,其中
,其中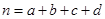 )
)
某工厂在试验阶段大量生产一种零件.这种零件有A,B两项技术指标需要检测,设各项技术指标达标与否互不影响.若有且仅有一项技术指标达标的概率为5/12,至少一项技术指标达标的概率为11/12.按质量检验规定:两项技术指标都达标的零件为合格品.
(1)求一个零件经过检测为合格品的概率是多少?
(2)任意依次抽出5个零件进行检测,求其中至多3个零件是合格品的概率是多少?
(3)任意依次抽取该种零件4个,设ξ表示其中合格品的个数,求Eξ与Dξ.
甲、乙两人独立地破译1个密码,他们能译出密码的概率分别为 和
和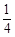 ,求
,求
(1)恰有1人译出密码的概率;
(2)若达到译出密码的概率为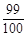 ,至少需要多少乙这样的人.
,至少需要多少乙这样的人.
一款击鼓小游戏的规则如下:每盘游戏都需要击鼓三次,每次击鼓要么出现一次音乐,要么不出现音乐;每盘游戏击鼓三次后,出现一次音乐获得10分,出现两次音乐获得20分,出现三次音乐获得100分,没有出现音乐则扣除200分(即获得-200分).设每次击鼓出现音乐的概率为,且各次击鼓出现音乐相互独立.
(1)设每盘游戏获得的分数为,求
的分布列;
(2)玩三盘游戏,至少有一盘出现音乐的概率是多少?
(3)玩过这款游戏的许多人都发现,若干盘游戏后,与最初的分数相比,分数没有增加反而减少了.请运用概率统计的相关知识分析分数减少的原因.
“蛟龙号”从海底中带回的某种生物,甲乙两个生物小组分别独立开展对该生物离开恒温箱的成活情况进行研究,每次试验一个生物,甲组能使生物成活的概率为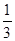 ,乙组能使生物成活的概率为
,乙组能使生物成活的概率为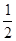 ,假定试验后生物成活,则称该试验成功,如果生物不成活,则称该次试验是失败的.
,假定试验后生物成活,则称该试验成功,如果生物不成活,则称该次试验是失败的.
(1)甲小组做了三次试验,求至少两次试验成功的概率;
(2)如果乙小组成功了4次才停止试验,求乙小组第四次成功前共有三次失败,且恰有两次连续失败的概率;
(3)若甲乙两小组各进行2次试验,设试验成功的总次数为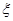 ,求
,求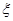 的期望.
的期望.
试题篮
()