高中数学正交试验设计方法试题

明天上午李明要参加义务劳动，为了准时起床，他用甲、乙两个闹钟叫醒自己，假设甲闹钟准时响的概率是0.80，乙闹钟准时响的概率是0.90，则两个闹钟至少有一准时响的概率是________．

甲、乙两人将参加某项测试，他们能达标的概率都是0.8，设随机变量为两人中能达标的人数，则的数学期望为        ．   

已知射手甲射击一次，命中9环（含9环）以上的概率为0.56，命中8环的概率为0.22，命中7环的概率为0.12．
①求甲射击一次，命中不足8环的概率.
②求甲射击一次，至少命中7环的概率.

某医院将一专家门诊已诊的1000例病人的病情及诊断所用时间（单位：分钟）进行了统计，如下表．若视频率为概率，请用有关知识解决下列问题．

病症及代号	普通病症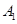	复诊病症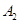	常见病症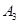	疑难病症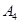	特殊病症
人数	100	300	200	300	100
每人就诊时间（单位：分钟）	3	4	5	6	7

用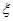表示某病人诊断所需时间，求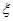的数学期望．
并以此估计专家一上午（按3小时计算）可诊断多少病人；
某病人按序号排在第三号就诊，设他等待的时间为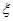，求；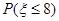
求专家诊断完三个病人恰好用了一刻钟的概率．

在4次独立试验中，事件A出现的概率相同，若事件A至少发生1次的概率是，则事件A 在一次试验中出现的概率是（   ）
12

A．	B．
C．	D．

设有升自来水，其中含有n个细菌，从中任取一升水检验，则这一升水中含有k个细菌的概率是        。

抛掷两颗骰子，所得点数之和为ξ，那么ξ＝4表示的随机试验结果是(　　)
A．两颗都是2点
B 一颗是3点，一颗是1点
C．两颗都是4点
D．一颗是3点，一颗是1点或两颗都是2点

在4次独立重复试验中事件A出现的概率相同，若事件A至少发生1次的概率为，则事件A在1次试验中出现的概率为________．

有甲，乙两个盒子，甲盒中装有2个小球，乙盒中装有3个小球，每次随机选取一个盒子并从中取出一个小球
（1）当甲盒中的球被取完时，求乙盒中恰剩下1个球的概率；
（2）当第一次取完一个盒子中的球时，另一个盒子恰剩下个球，求的分布列及期望。

下面随机变量X的分布列不属于二项分布的是________．
①据中央电视台新闻联播报道，下周内在某网站下载一次数据，电脑被感染某种病毒的概率是0.65.设在这一周内，某电脑从该网站下载数据n次中被感染这种病毒的次数为X；②某射手射击击中目标的概率为p，设每次射击是相互独立的，从开始射击到击中目标所需要的射击次数为X；③某射手射击击中目标的概率为p，设每次射击是相互独立的，射击n次命中目标的次数为X；④位于某汽车站附近有一个加油站，汽车每次出站后到这个加油站加油的概率为0.6，国庆节这一天有50辆汽车开出该站，假设一天里汽车去该加油站加油是相互独立的，去该加油站加油的汽车数为X.

某次知识竞赛规则如下：在主办方预设的5个问题中，选手若能连续正确回答出两个问题，即停止答题，晋级下一轮．假设某选手正确回答每个问题的概率都是0.8，且每个问题的回答结果相互独立，则该选手恰好回答了4个问题就晋级下一轮的概率等于________．

某一批花生种子，如果每1粒发芽的概率为,那么播下4粒种子恰有2粒发芽的概率是                   . （请用分数表示结果）

“低碳经济”是促进社会可持续发展的推进器.某企业现有100万元资金可用于投资，如果投资“传统型”经济项目，一年后可能获利20%，可能损失10%,也可能不赔不赚，这三种情况发生的概率分别为；如果投资“低碳型”经济项目，一年后可能获利30%,也
可能损失20%，这两种情况发生的概率分别为a和n (其中a + b =1 )如果把100万元投资“传统型”经济项目，用表示投资收益（投资收益=回收资金一投资资金)，求的概率分布及均值（数学期望）；(II)如果把100万元投资“低碳型”经济项目，预测其投资收益均值会不低于投资“传统型”经济项目的投资收益均值，求a的取值范围

2011.年广州亚运会的一组志愿者全部通晓中文，并且每个志愿者还都通晓英语、日语和韩语中的一种（但无人通晓两种外语).已知从中任抽一人，其通晓中文和英语的概率为，通晓中文和日语的概率为.若通晓中文和韩语的人数不超过3人.
(I )求这组志愿者的人数；
(II)现从这组志愿者中选出通晓英语的志愿者1名，通晓韩语的志愿者1名，若甲通晓英语，乙通晓韩语，求甲和乙不全被选中的概率.

设随机变量，则________．