高中数学平面解析几何的产生──数与形的结合试题

椭圆上一点M到左焦点的距离为2，N是M的中点则（  ）
A    32     B  16    C  8       D  4

已知曲线的极坐标方程为，直线的参数方程是：  .
（Ⅰ）求曲线的直角坐标方程，直线的普通方程；
（Ⅱ）求曲线与直线交与两点，求长.

已知双曲线的焦点为F₁、F₂， 点M在双曲线上且则点M到x轴的距离为(    )

A．

B．

C．

D．

已知为椭圆的两个焦点，过的直线交椭圆于两点，若，则=       

已知为椭圆的两个焦点，过的直线交椭圆于A、B两点若，则=______

（本小题满分14分）
已知点、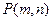,()是曲线C上的两点，点、关于轴对称，直线、分别交轴于点和点，
（Ⅰ）用、、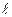、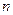分别表示和;
（Ⅱ）某同学发现，当曲线C的方程为：时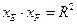，是一个定值与点、、的位置无关；请你试探究当曲线C的方程为：时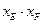， 的值是否也与点M、N、P的位置无关；
（Ⅲ）类比（Ⅱ）的探究过程，当曲线C的方程为时，探究与经加、减、乘、除的某一种运算后为定值的一个正确结论.(只要求写出你的探究结论，无须证明).

(本题满分14分)设点F（0,2），曲线C上任意一点M（x,y）满足以线段FM为直径的圆与x 轴相切.
（1）求曲线C的方程；
（2）设过点Q（0，－2）的直线l与曲线C交于A,B两点，问|FA|,|AB|,|FB|能否成等差数列？若能，求出直线l的方程；若不能，请说明理由.

中心在原点，其中一个焦点为（－2,0），且过点（2,3），则该椭圆方程为             ；

经过圆的圆心C，且与直线垂直的直线方程是 （   ）

A．x＋y＋1＝0

B．x＋y－1＝0

C．x－y＋1＝0

D．x－y－1＝0

（本小题满分12分）
扇形中，半径°，在的延长线上有一动点，过点作与半圆弧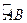相切于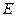点，且与过点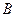所作的的垂线交于点，此时显然有CO=CD，DB=DE，问当OC多长时，直角梯形面积最小，并求出这个最小值。

（本小题满分14分）
设圆满足条件：（1）截y轴所得的弦长为2；（2）被x轴分成两段弧，其弧长的比为3︰1；（3）圆心到直线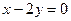：的距离为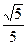．求这个圆的方程．

（本小题满分12分）
已知点A（15，0），点P是圆上的动点，M为线段PA的中点，当点P在圆上运动时，求动点M的轨迹方程．

过点A 与圆相切的直线方程是              ．

在圆上等可能的任取一点A，以OA（O为坐标原点）为终边的角为，则使的概率为（   ）

A．

B．

C．

D．

若圆截直线得弦长为，则a的值为(  )

A．-2或2

B．

C．2或0

D．-2或0