以直角坐标系的原点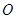 为极点,
为极点,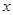 轴的正半轴为极轴,已知点
轴的正半轴为极轴,已知点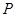 的直角坐标为
的直角坐标为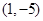 ,点
,点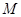 的极坐标为
的极坐标为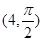 ,若直线
,若直线 过点
过点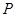 ,且倾斜角为
,且倾斜角为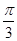 ,圆
,圆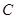 以
以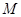 为 圆心、
为 圆心、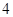 为半径。
为半径。
(I) 写出直线 的参数方程和圆
的参数方程和圆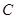 的极坐标方程;
的极坐标方程;
(Ⅱ)试判定直线 和圆
和圆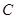 的位置关系。
的位置关系。
设过点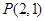 的直线
的直线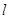 分别与
分别与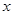 正半轴,
正半轴, 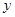 轴正半轴交于
轴正半轴交于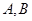 两点,
两点,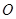 为坐标原点,则三角形
为坐标原点,则三角形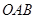 面积最小时直线方程为
面积最小时直线方程为
已知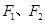 分别是双曲线
分别是双曲线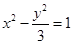 的左、右焦点,过
的左、右焦点,过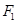 斜率为
斜率为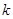 的直线
的直线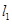 交双曲线的左、右两支分别于
交双曲线的左、右两支分别于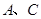 两点,过
两点,过 且与
且与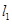 垂直的直线
垂直的直线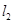 交双曲线的左、右两支分别于
交双曲线的左、右两支分别于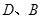 两点。
两点。
(1)求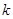 的取值范围;
的取值范围;
求四边形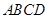 面积的最小值。
面积的最小值。
试题篮
()