如图,给出定点A(a,0) (a>0,a≠1)和直线l:x=-1,B是直线l上的动点,∠BOA的角平分线交AB于点C,求点C的轨迹方程,并讨论方程表示的曲线类型与a值的关系.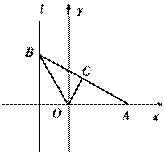
设曲线C的方程是y=x3-x,将C沿x轴、y轴正向分别平移t、s单位长度后,得到曲线C1.
(1)写出曲线C1的方程;
(2)证明:曲线C与C1关于点A( ,
, )对称.
)对称.
关于曲线 :
: 的下列说法:①关于原点对称;②关于直线
的下列说法:①关于原点对称;②关于直线 对称;③是封闭图形,面积大于
对称;③是封闭图形,面积大于 ;④不是封闭图形,与圆
;④不是封闭图形,与圆 无公共点;⑤与曲线D:
无公共点;⑤与曲线D: 的四个交点恰为正方形的四个顶点,其中正确的序号是 .
的四个交点恰为正方形的四个顶点,其中正确的序号是 .
试题篮
()