如图,动点M与两定点A(-1,0),B(2,0)构成△MAB,且∠MBA=2∠MAB.设动点M的轨迹为C.
(1)求轨迹C的方程;
(2)设直线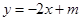 (其中
(其中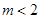 )与y轴相交于点P,与轨迹C相交于点Q,R,且
)与y轴相交于点P,与轨迹C相交于点Q,R,且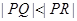 ,求
,求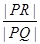 的取值范围.
的取值范围.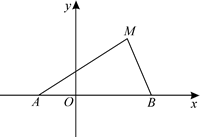
设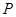 是曲线
是曲线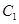 上的任一点,
上的任一点, 是曲线
是曲线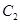 上的任一点,称
上的任一点,称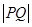 的最小值为曲线
的最小值为曲线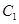 与曲线
与曲线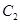 的距离.
的距离.
(1)求曲线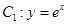 与直线
与直线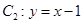 的距离;
的距离;
(2)设曲线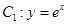 与直线
与直线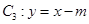 (
(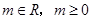 )的距离为
)的距离为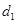 ,直线
,直线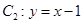 与直线
与直线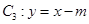 的距离为
的距离为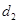 ,求
,求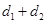 的最小值.
的最小值.
已知椭圆的离心率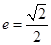 ,左、右焦点分别为
,左、右焦点分别为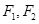 ,定点P
,定点P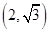 ,点
,点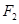 在线段
在线段 的中垂线上.
的中垂线上.
(1)求椭圆C的方程;
(2)设直线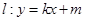 与椭圆C交于M、N两点,直线
与椭圆C交于M、N两点,直线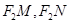 的倾斜角分别为
的倾斜角分别为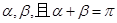 ,求证:直线
,求证:直线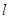 过定点,并求该定点的坐标.
过定点,并求该定点的坐标.
已知椭圆的中心在坐标原点O,焦点在x轴上,椭圆的短轴端点和焦点所组成的四边形为正方形,两准线间的距离为4.
(Ⅰ)求椭圆的方程;
(Ⅱ)直线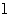 过点P(0,2)且与椭圆相交于A、B两点,当ΔAOB面积取得最大值时,求直线l的方程.
过点P(0,2)且与椭圆相交于A、B两点,当ΔAOB面积取得最大值时,求直线l的方程.
圆C与y轴相切,圆心在射线 x-3y=0(x>0)上,且圆C截直线y=x所得弦长为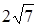 . (1)求圆C的方程。(2)点P(x,y)是圆C上的动点,求x+y的最大值。(3)求过点M(2,1)的圆的弦的中点轨迹方程。
. (1)求圆C的方程。(2)点P(x,y)是圆C上的动点,求x+y的最大值。(3)求过点M(2,1)的圆的弦的中点轨迹方程。
如右图,在平面直角坐标系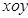 中,已知“葫芦”曲线
中,已知“葫芦”曲线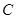 由圆弧
由圆弧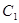 与圆弧
与圆弧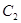 相接而成,两相接点
相接而成,两相接点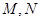 均在直线
均在直线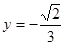 上.圆弧
上.圆弧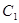 所在圆的圆心是坐标原点
所在圆的圆心是坐标原点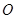 ,半径为
,半径为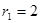 ;圆弧
;圆弧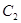 过点
过点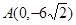 .
.
(I)求圆弧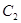 的方程;
的方程;
(II)已知直线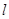 :
: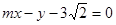 与“葫芦”曲线
与“葫芦”曲线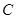 交于
交于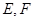 两点.当
两点.当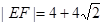 时,求直线
时,求直线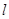 的方程.
的方程.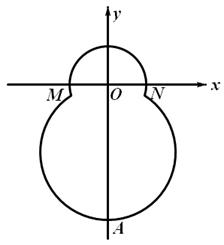
(本题满分16分)本题共有2个小题,第1小题满分6分,第2小题满分10分.
已知两点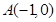 、
、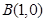 ,点
,点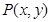 是直角坐标平面上的动点,若将点
是直角坐标平面上的动点,若将点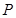 的横坐标保持不变、纵坐标扩大到
的横坐标保持不变、纵坐标扩大到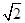 倍后得到点
倍后得到点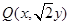 满足
满足 .
.
(1) 求动点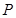 所在曲线
所在曲线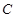 的轨迹方程;
的轨迹方程;
(2)(理科)过点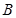 作斜率为
作斜率为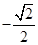 的直线
的直线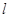 交曲线
交曲线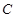 于
于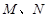 两点,且满足
两点,且满足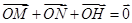 ,又点
,又点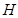 关于原点O的对称点为点
关于原点O的对称点为点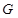 ,试问四点
,试问四点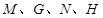 是否共圆,若共圆,求出圆心坐标和半径;若不共圆,请说明理由.
是否共圆,若共圆,求出圆心坐标和半径;若不共圆,请说明理由.
(文科)过点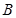 作斜率为
作斜率为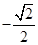 的直线
的直线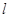 交曲线
交曲线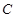 于
于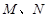 两点,且满足
两点,且满足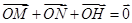 (O为坐标原点),试判断点
(O为坐标原点),试判断点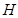 是否在曲线
是否在曲线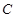 上,并说明理由.
上,并说明理由.
已知椭圆C: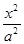 +
+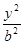 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=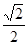 ,左、右焦点分别为F1、F2,点P(2,
,左、右焦点分别为F1、F2,点P(2,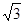 ),点F2在线段PF1的中垂线上.
),点F2在线段PF1的中垂线上.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线l:y=kx+m与椭圆C交于M、N两点,直线F2M与F2N的倾斜角分别为α,β,且α+β=π,试问直线l是否过定点?若过,求该定点的坐标.
(本小题满分14分)设椭圆 的左右焦点分别为
的左右焦点分别为 ,离心率
,离心率 ,点
,点 在直线
在直线 :
: 的左侧,且F2到l的距离为
的左侧,且F2到l的距离为 。
。 (1)求
(1)求 的值;
的值;
(2)设 是
是 上的两个动点,
上的两个动点,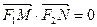 ,证明:当
,证明:当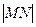 取最小值时,
取最小值时,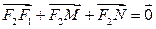 。
。
四、选考题(本小题满分10分)
请考生在第(22)、(23)、(24)三题中任选一题做答,如果多做,则按所做的第一题记分.答时用2B铅笔在答题卡上把所选题目的题号涂黑.
22.选修4-1:几何证明选讲
在 中,AB=AC,过点A的直线与其外接圆交于点P,交BC延长线于点D。
中,AB=AC,过点A的直线与其外接圆交于点P,交BC延长线于点D。
(1)求证:  ;
;
(2)若AC=3,求 的值。
的值。
如图,已知椭圆的中心在坐标原点,焦点在 轴上,它的一个顶点为
轴上,它的一个顶点为 ,且离心率等于
,且离心率等于 ,过点
,过点 的直线
的直线 与椭圆相交于不同两点
与椭圆相交于不同两点 ,点
,点 在线段
在线段 上。
上。
(1)求椭圆的标准方程;
(2)设 ,若直线
,若直线 与
与 轴不重合,
轴不重合,
试求 的取值范围。
的取值范围。
试题篮
()