已知椭圆C: +
+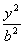 =1(a>b>0)的左.右焦点为F1、F2,离心率为e. 直线l:y=ex+a与x轴.y轴分别交于点A、B,M是直线l与椭圆C的一个公共点,P是点F1关于直线l的对称点,设
=1(a>b>0)的左.右焦点为F1、F2,离心率为e. 直线l:y=ex+a与x轴.y轴分别交于点A、B,M是直线l与椭圆C的一个公共点,P是点F1关于直线l的对称点,设 =λ
=λ .
.
(Ⅰ)证明:λ=1-e2;
(Ⅱ)确定λ的值,使得△PF1F2是等腰三角形.
(本小题满分15分) 如图,已知圆O:x2+y2=2交x轴于A,B两点,曲线C是以AB为长轴,离心率为
如图,已知圆O:x2+y2=2交x轴于A,B两点,曲线C是以AB为长轴,离心率为 的椭圆,其右焦点为F.若点P(-1,1)为圆O上一点,连结PF,过原点O作直线PF的垂线交椭圆C的右准线l于点Q.(1)求椭圆C的标准方程;
的椭圆,其右焦点为F.若点P(-1,1)为圆O上一点,连结PF,过原点O作直线PF的垂线交椭圆C的右准线l于点Q.(1)求椭圆C的标准方程;
(2)证明:直线PQ与圆O相切.
(本小题满分12分)
已知点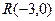 ,点
,点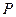 在
在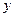 轴上,点
轴上,点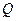 在
在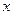 轴的正半轴上,点
轴的正半轴上,点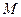 在直线
在直线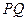 上,且
上,且
满足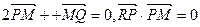 .
.
(Ⅰ)当点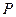 在
在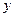 轴上移动时,求点
轴上移动时,求点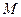 的轨迹
的轨迹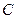 的方程;
的方程;
(Ⅱ)设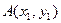 、
、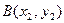 为轨迹
为轨迹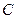 上两点,且
上两点,且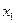 >1,
>1, 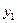 >0,
>0,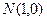 ,求实数
,求实数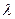 ,
,
使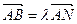 ,且
,且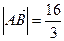 .
.
已知椭圆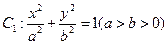 的离心率为
的离心率为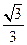 ,直线
,直线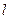 :
: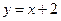 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆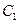 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切.
(I)求椭圆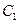 的方程;
的方程;
(II)设椭圆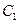 的左焦点为
的左焦点为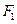 ,右焦点
,右焦点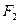 ,直线
,直线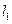 过点
过点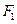 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线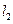 垂直
垂直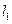 于点
于点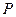 ,线段
,线段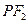 垂直平分线交
垂直平分线交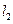 于点
于点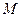 ,求点
,求点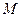 的轨迹
的轨迹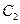 的方程;
的方程;
(III)设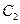 与
与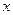 轴交于点
轴交于点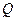 ,不同的两点
,不同的两点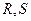 在
在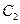 上,且满足
上,且满足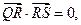 求
求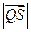 的取值范围.
的取值范围.
(本小题满分12分)
|
已知点A是抛物线y2=2px(p>0)上一点,F为抛物线的焦点,准线l与x轴交于点K,已知|AK|=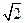 |AF|,三角形AFK的面积等于8.
|AF|,三角形AFK的面积等于8.
(本小题满分13分)如图,在矩形ABCD中,已知A(2,0)、C(-2,2),点P在BC边上移动,线段OP的垂直平分线交y轴于点E,点M满足
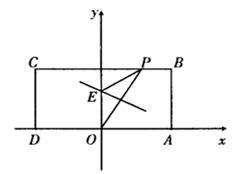
(Ⅰ)求点M的轨迹方程;
(Ⅱ)已知点F(0,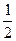 ),过点F的直线l交点M的轨迹于Q、R两点,且
),过点F的直线l交点M的轨迹于Q、R两点,且 求实数
求实数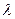 的取值范围.
的取值范围.
已知点 是中心在原点,长轴在x轴上的椭圆的一个顶点,离心率为
是中心在原点,长轴在x轴上的椭圆的一个顶点,离心率为 ,椭圆的左右焦点分别为F1和F2 。
,椭圆的左右焦点分别为F1和F2 。
(Ⅰ)求椭圆方程;
(Ⅱ)点M在椭圆上,求⊿MF1F2面积的最大值;
(Ⅲ)试探究椭圆上是否存在一点P,使 ,若存在,请求出点P的坐标;若不存在,请说明理由。
,若存在,请求出点P的坐标;若不存在,请说明理由。
(本题满分13分) 已知椭圆 的中心在坐标原点,焦点在坐标轴上,且经过
的中心在坐标原点,焦点在坐标轴上,且经过 、
、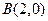 、
、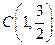 三点. (1)求椭圆
三点. (1)求椭圆 的方程:(2)若点D为椭圆
的方程:(2)若点D为椭圆 上不同于
上不同于 、
、 的任意一点,
的任意一点, ,当
,当 内切圆的面积最大时。求内切圆圆心的坐标;(3)若直线
内切圆的面积最大时。求内切圆圆心的坐标;(3)若直线 与椭圆
与椭圆 交于
交于 、
、 两点,证明直线
两点,证明直线 与直线
与直线 的交点在定直线上并求该直线的方程.
的交点在定直线上并求该直线的方程.
如图,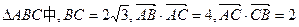 ,双曲线M是以B、C为焦点且过A点.
,双曲线M是以B、C为焦点且过A点. (Ⅰ)建立适当的坐标系,求双曲线M的方程;
(Ⅰ)建立适当的坐标系,求双曲线M的方程;
(Ⅱ)设过点E(1,0)的直线l分别与双曲线M的左、右支交于
F、G两点,直线l的斜率为k,求k的取值范围.;
(Ⅲ)对于(II)中的直线l,是否存在k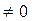 使|OF|=|OG|
使|OF|=|OG|
若有求出k的值,若没有说明理由.(O为原点)
如图,给出定点A(a,0) (a>0,a≠1)和直线l:x=-1,B是直线l上的动点,∠BOA的角平分线交AB于点C,求点C的轨迹方程,并讨论方程表示的曲线类型与a值的关系.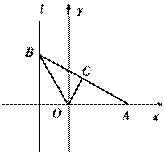
试题篮
()