( 10分)已知双曲线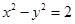 的左、右焦点分别为
的左、右焦点分别为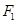 ,
, ,过点
,过点 的动直线与双曲线相交于
的动直线与双曲线相交于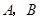 两点.
两点.
(I)若动点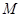 满足
满足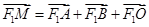 (其中
(其中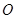 为坐标原点),求点
为坐标原点),求点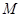 的轨迹方程;
的轨迹方程;
(II)在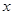 轴上是否存在定点
轴上是否存在定点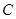 ,使
,使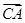 ·
·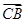 为常数?若存在,求出点
为常数?若存在,求出点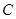 的坐标;
的坐标;
若不存在,请说明理由.
已知曲线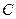 的极坐标方程为
的极坐标方程为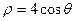 ,直线
,直线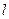 的参数方程是:
的参数方程是: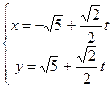
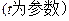 .
.
(Ⅰ)求曲线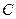 的直角坐标方程,直线
的直角坐标方程,直线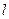 的普通方程;
的普通方程;
(Ⅱ)将曲线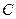 横坐标缩短为原来的
横坐标缩短为原来的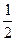 ,再向左平移1个单位,得到曲线曲线
,再向左平移1个单位,得到曲线曲线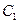 ,求曲线
,求曲线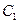 上的点到直线
上的点到直线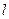 距离的最小值.
距离的最小值.
已知点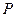 为圆周
为圆周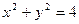 的动点,过
的动点,过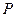 点作
点作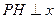 轴,垂足为
轴,垂足为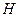 ,设线段
,设线段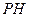 的中点为
的中点为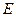 ,记点
,记点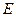 的轨迹方程为
的轨迹方程为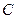 ,点
,点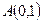
(1)求动点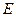 的轨迹方程
的轨迹方程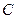 ;
;
(2)若斜率为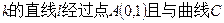 的另一个交点为
的另一个交点为 ,求
,求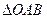 面积的最大值及此时直线
面积的最大值及此时直线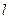 的方程;
的方程;
(3)是否存在方向向量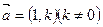 的直线
的直线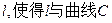 交与两个不同的点
交与两个不同的点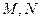 ,且有
,且有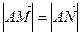 ?若存在,求出
?若存在,求出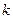 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
试题篮
()