在平面直角坐标系中,两点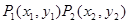 间的“L-距离”定义为
间的“L-距离”定义为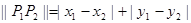 ,则平面内与
,则平面内与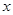 轴上两个不同的定点
轴上两个不同的定点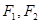 的“L-距离”之和等于定值(大于
的“L-距离”之和等于定值(大于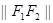 )的点的轨迹可以是( )
)的点的轨迹可以是( )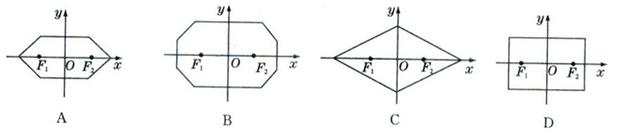
如图,动点M与两定点A(-1,0),B(2,0)构成△MAB,且∠MBA=2∠MAB.设动点M的轨迹为C.
(1)求轨迹C的方程;
(2)设直线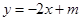 (其中
(其中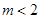 )与y轴相交于点P,与轨迹C相交于点Q,R,且
)与y轴相交于点P,与轨迹C相交于点Q,R,且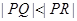 ,求
,求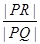 的取值范围.
的取值范围.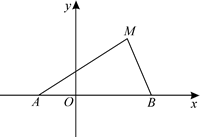
在平面直角坐标系中,两点间的"
距离"定义为
则平面内与
轴上两个不同的定点
的"
距离"之和等于定值(大于
)的点的轨迹可以是()
| A. |
|
B. |
|
| C. |
|
D. |
|
设 为曲线
为曲线
 上的点,且曲线
上的点,且曲线 在点
在点 处切线倾斜角的取值范围是(
处切线倾斜角的取值范围是(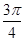 ,
, ),则点
),则点 横坐标的取值范围为( )
横坐标的取值范围为( )
A. |
B.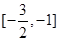 |
C.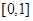 |
D. |
设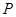 是曲线
是曲线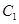 上的任一点,
上的任一点, 是曲线
是曲线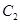 上的任一点,称
上的任一点,称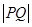 的最小值为曲线
的最小值为曲线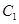 与曲线
与曲线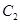 的距离.
的距离.
(1)求曲线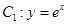 与直线
与直线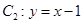 的距离;
的距离;
(2)设曲线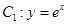 与直线
与直线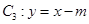 (
(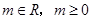 )的距离为
)的距离为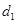 ,直线
,直线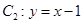 与直线
与直线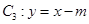 的距离为
的距离为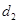 ,求
,求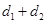 的最小值.
的最小值.
互相平行的三条直线,最多可以确定的平面个数为( )
| A.1个 | B.2个 | C.3个 | D.4个 |
已知命题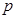 : 双曲线的离心率小于1. 则
: 双曲线的离心率小于1. 则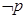 为
为
| A.双曲线的离心率大于1 | B.有的双曲线离心率小于1 |
| C.有的双曲线离心率大于1 | D.存在双曲线, 其离心率不小于1 |
已知椭圆的离心率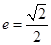 ,左、右焦点分别为
,左、右焦点分别为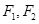 ,定点P
,定点P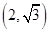 ,点
,点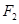 在线段
在线段 的中垂线上.
的中垂线上.
(1)求椭圆C的方程;
(2)设直线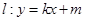 与椭圆C交于M、N两点,直线
与椭圆C交于M、N两点,直线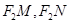 的倾斜角分别为
的倾斜角分别为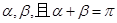 ,求证:直线
,求证:直线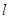 过定点,并求该定点的坐标.
过定点,并求该定点的坐标.
试题篮
()