某种种子每粒发芽的概率都为0.9,现播种了1000粒,对于没有发芽的种子,每粒需再补种2粒,补种的种子数记为 ,则 的数学期望为( ).
| A. | 100 | B. | 200 | C. | 300 | D. | 400 |
在“信阳市中学生歌手大赛”比赛现场上七位评委为某选手打出的分数的茎叶统计图如图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )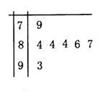
A.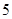 和 和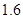 |
B. 和 和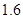 |
C. 和 和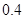 |
D.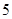 和 和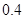 |
甲乙两人进行乒乓球比赛,约定每局胜者得1分,负者得0分,比赛进行到有一人比对方多2分或打满6局时停止.设甲在每局中获胜的概率为 ,乙在每局中获胜的概率为
,乙在每局中获胜的概率为 ,且各局胜负相互独立,则比赛停止时已打局数
,且各局胜负相互独立,则比赛停止时已打局数 的期望
的期望 为 ( )
为 ( )
A. |
B. |
C. |
D. |
如图,将一个各面都涂了油漆的正方体,切割为125个同样大小的小正方体,经过搅拌后,从中随机取一个小正方体,记它的油漆面数为X,则X的均值E(X)等于( ).
A. |
B. |
C. |
D. |
数据x1,x2,…,xn平均数为6,标准差为2,则数据2x1-6,2x2-6,…,2xn-6的平均数与方差分别为( ).
| A.6,16 | B.12,8 | C.6,8 | D.12,16 |
签盒中有编号为1、2、3、4、5、6的六支签,从中任意取3支,设X为这3支签的号码之中最大的一个,则X的数学期望为( )
| A.5 | B.5.25 | C.5.8 | D.4.6 |
红队队员甲、乙、丙与蓝队队员
进行围棋比赛,甲对
,乙对
,丙对
各一盘,已知甲胜
,乙胜
,丙胜
的概率分别为0.6,0.5,0.5,假设各盘比赛结果相互独立.
(Ⅰ)求红队至少两名队员获胜的概率;
(Ⅱ)用
表示红队队员获胜的总盘数,求
的分布列和数学期望
.
同时抛掷 枚均匀的硬币
枚均匀的硬币 次,设
次,设 枚硬币正好出现
枚硬币正好出现 枚正面向上,
枚正面向上, 枚反面向上的次数为
枚反面向上的次数为 ,则
,则 的数学期望是( )
的数学期望是( )
A. |
B. |
C. |
D. |
一支足球队每场比赛获胜(得3分)的概率为a,与对手踢平(得1分)的概率为b,负于对手(得0分)的概率为 ,已知该足球队进行一场比赛得分的期望是1,则
,已知该足球队进行一场比赛得分的期望是1,则 的最小值为 ( )
的最小值为 ( )
A. |
B. |
C. |
D. |
如果数据x1,x2,x3,…,xn的平均数为 ,方差为62,则数据3x1+5,3x2+5,…,3xn+5的平均数和方差分别是( )
,方差为62,则数据3x1+5,3x2+5,…,3xn+5的平均数和方差分别是( )
A. |
B. |
C. |
D. |
为了稳定市场,确保农民增收,某农产品3月以后的每月市场收购价格与其前三个月的市场收购价格有关,并使其与前三个月的市场收购价格之差的平方和最小,下表列出的是该产品今年前六个月的市场收购价格:
| 月份 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 价格(元/担) |
68 |
78 |
67 |
71 |
72 |
70 |
|
则前七个月该产品的市场收购价格的方差为
A. B.
B. C.11 D.
C.11 D.
计算机考试分理论考试与实际操作考试两部分进行,每部分考试成绩只记“合格”与“不合格”,两部分考试都“合格”者,则计算机考试“合格“并颁发”合格证书“.甲、乙、丙三人在理论考试中“合格”的概率依次为 ,在实际操作考试中“合格”的概率依次为
,在实际操作考试中“合格”的概率依次为 ,所有考试是否合格相互之间没有影响。
,所有考试是否合格相互之间没有影响。
(1)假设甲、乙、丙3人同时进行理论与实际操作两项考试,谁获得“合格证书”的可能性大?
(2)求这3人进行理论与实际操作两项考试后,恰有2人获得“合格证书”的概率;
(3)用X表示甲、乙、丙3人计算机考试获“合格证书”的人数,求X的分布列和数学期望EX。
试题篮
()