高中数学随机思想的发展解答题

甲班有2名男乒乓球选手和3名女乒乓球选手，乙班有3名男乒乓球选手和1名女乒乓球选手，学校计划从甲乙两班各选2名选手参加体育交流活动.
（Ⅰ）求选出的4名选手均为男选手的概率.
（Ⅱ）记为选出的4名选手中女选手的人数，求的分布列和期望.

小王参加一次比赛，比赛共设三关，第一、二关各有两个必答题，如果每关两个问题都答对，可进入下一关，第三关有三个问题，只要答对其中两个问题，则闯关成功．每过一关可一次性获得价值分别为1000元，3000元，6000元的奖品(不重复得奖)，小王对三关中每个问题回答正确的概率依次为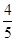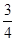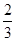，，，且每个问题回答正确与否相互独立．
(1)求小王过第一关但未过第二关的概率；
(2)用X表示小王所获得奖品的价值，写出X的概率分布列，并求X的数学期望．

（本小题满分12分）在第9届校园文化艺术节棋类比赛项目报名过程中，我校高二(2)班共有16名男生和14名女生预报名参加，调查发现，男、女选手中分别有10人和6人会围棋.
（I）根据以上数据完成以下22列联表：

	会围棋	不会围棋	总计
男
女
总计			30

并回答能否在犯错的概率不超过0．10的前提下认为性别与会围棋有关？
参考公式：其中n=a+b+c+d
参考数据：

	0.40	0.25	0.10	0.010
	0.708	1.323	2.706	6.635

（Ⅱ）若从会围棋的选手中随机抽取3人成立该班围棋代表队，则该代表队中既有男又
有女的概率是多少？
（Ⅲ）若从14名女棋手中随机抽取2人参加棋类比赛，记会围棋的人数为，求的期望.

心理学家分析发现视觉和空间能力与性别有关， 某数学兴趣小组为了 验 证这个结论，从兴趣小组中按分层抽样的方法抽取50名同学 （男30女20）， 给所有同学几何题和代数题各一题， 让各位同学自由选择一道题进行解答．选题情况如下表：（单位：人）

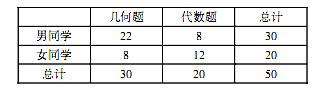
（Ⅰ）能否据此判断有97．5%的把握认为视觉和空间能力与性别有关？
（Ⅱ）经过多次测试后，甲每次解答一道几何题所用的时间在5—7分钟，乙每次解答一道几何题所用
的时间在6—8分钟，现甲、乙各解同一道几何题，求乙比甲先解答完的概率．
（Ⅲ）现从选择做几何题的8名女生中任意抽取两人对她们的答题情况进行全程研究，记甲、 乙两女
生被抽到的人数为X， 求X的分布列及数学期望E（X） ．
附表及公式

（本小题满分12分）
某校从6名学生会干部（其中男生4人，女生2人）中选3人参加市中学生运动会志愿者.
（Ⅰ）所选3人中女生人数为ξ，求ξ的分布列及数学期望.
（Ⅱ）在男生甲被选中的情况下，求女生乙也被选中的概率.

随机抽取某厂的某种产品100件，经质检，其中有一等品63件、二等品25件、三等品10件、次品2件．已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元，而1件次品亏损2万元．设1件产品的利润（单位：万元）为．
（1）求的分布列；
（2）求1件产品的平均利润（即的数学期望）；
（3）经技术革新后，仍有四个等级的产品，但次品率降为，一等品率提高为．如果此时要求1件产品的平均利润不小于5.13万元，则三等品率最多是多少？

（本小题满分12分）从装有2只红球，2只白球和1只黑球的袋中逐一取球，已知每只球被抽取的可能性相同。
（1）若抽取后又放回，抽3次，①分别求恰2次为红球的概率及抽全三种颜色球的概率；②求抽到红球次数的数学期望．
（2）若抽取后不放回，抽完红球所需次数为的分布列及期望．

在2014年11月4日宜宾市举办的四川省第十四届少数民族传统体育运动会的餐饮点上，某种茶饮料一天的销售量与该天的日平均气温（单位：℃）有关，若日平均气温不超过15 ℃，则日销售量为100瓶；若日平均气温超过15℃但不超过20 ℃，则日销售量为150 瓶；若日平均气温超过20 ℃，则日销售量为200瓶．据宜宾市气象部门预测，该地区在运动会期间每一天日平均气温不超过15 ℃，超过15 ℃但不超过20 ℃，超过20 ℃这三种情况发生的概率分别为，又知P₁，P₂为方程5x²－3x＋a＝0的两根，且．
（1）求P₁，P₂，P₃的值；
（2）记ξ表示该茶饮料在运动会期间任意两天的销售量总和（单位：瓶），求的分布列及数学期望．

某电视台组织部分记者，用“10分制”随机调查某社区居民的幸福指数.现从调查人群中随机抽取16名，如图所示的茎叶图记录了他们的幸福指数的得分(以小数点前的一位数字为茎，小数点后的一位数字为叶)：

（1）指出这组数据的众数和中位数；
（2）若幸福指数不低于9.5分，则称该人的幸福指数为“极幸福”.求从这16人中随机选取3人，至多有1人是“极幸福”的概率；
（3）以这16人的样本数据来估计整个社区的总体数据，若从该社区(人数很多)任选3人，记表示抽到“极幸福”的人数，求的分布列及数学期望．

某校举办安全法规知识竞赛，从参赛的高一、高二学生中各抽出100人的成绩作为样本．对高一年级的100名学生的成绩进行统计，得到成绩分布的频率分布直方图如图：

（1）若规定60分以上（包括60分）为合格，计算高一年级这次知识竞赛的合格率；
（2）将上述调查所得到的频率视为概率.现在从该校大量高一学生中，采用随机抽样方法每次抽取1名学生，抽取3次，记被抽取的3名学生中的合格人数为.若每次抽取的结果是相互独立的，求的分布列和期望；

	高一	高二	合计
合格人数
不合格人数
合计

 
（3）若高二年级这次知识竞赛的合格率为60%，由以上统计数据填写2×2列联表，并问是否有99%的把握认为“这次知识竞赛的成绩与年级有关系” ．

山东省实验中学为了活跃师生的课外文化生活，在2015年3月中旬举办了一次知识竞赛，经过层层筛选，最后五名同学进入了总决赛．在进行笔答题知识竞赛中，最后一个大题是选做题，要求参加竞赛的五名选手从2道题中选做一道进行解答，假设这5位选手选做每一题的可能性均为，求
（Ⅰ）其中甲乙2位选手选做同一道题的概率．
（Ⅱ）设这5位选手中选做第1题的人数为x，求x的分布列及数学期望．

某联欢晚会举行抽奖活动，举办方设置了甲、乙两种抽奖方案，方案甲的中奖率为，中奖可以获得2分；方案乙的中奖率为，中奖可以获得3分；未中奖则不得分。每人有且只有一次抽奖机会，每次抽奖中奖与否互不影响，晚会结束后凭分数兑换奖品。
（1）若小明选择方案甲抽奖，小红选择方案乙抽奖，记他们的累计得分为,求的概率；
（2）若小明、小红两人都选择方案甲或都选择方案乙进行抽奖，问：他们选择何种方案抽奖，累计得分的数学期望较大？

（本小题满分12分）设和分别是先后抛掷一枚骰子得到的点数，用随机变量表示函数的极值点的个数．
（Ⅰ）求函数有极值的概率；
（Ⅱ）求的分布列和数学期望；
（Ⅲ）求在先后两次出现的点数中有5的条件下，函数有极值的概率．

甲、乙、丙三人进行羽毛球练习赛，其中两人比赛，另一人当裁判，每局比赛结束时，负的一方在下一局当裁判.设各局中双方获胜的概率均为，各局比赛的结束相互独立，第1局甲当裁判.
（1）求第4局甲当裁判的概率；
（2）X表示前4局中乙当裁判的次数，求X的数学期望.

下图是某市3月1日至14日的空气质量指数趋势图，空气质量指数小于100表示空气质量优良，空气质量指数大于200表示空气重度污染，某人随机选择3月1日至3月13日中的某一天到达该市，并停留2天

（1）求此人到达当日空气重度污染的概率
（2）设X是此人停留期间空气质量优良的天数，求X的分布列与数学期望.
（3）由图判断从哪天开始连续三天的空气质量指数方差最大？（结论不要求证明）