高中数学随机思想的发展解答题

（本小题满分12分）甲、乙两袋中各装有大小相同的小球9个，其中甲袋中红色、黑色、白色小球的个数分别为2，3，4，乙袋中红色、黑色、白色小球的个数均为3，某人用左右手分别从甲、乙两袋中取球.
（Ⅰ）若左右手各取一球，求两只手中所取的球颜色不同的概率；
（Ⅱ）若左右手依次各取两球，称同一手中 两球颜色相同的取法为成功取法，记两次取球（左右手依次各取两球为两次取球）的成功取法次数为随机变量X，求X的分布列和数学期望.

根据以往的成绩记录，甲、乙两名队员射击击中目标靶的环数的频率分布情况如图所示.

假设每名队员每次射击相互独立.
（Ⅰ）求上图中的值；
（Ⅱ）队员甲进行三次射击，求击中目标靶的环数不低于8环的次数的分布列及数学期望（频率当作概率使用）；
（Ⅲ）由上图判断，在甲、乙两名队员中，哪一名队员的射击成绩更稳定？（结论不需证明）

（本小题满分13分）国家环境标准制定的空气质量指数（简称AQI）与空气质量等级对应关系如下表：

空气质量等级	优	良	轻度污染	中度污染	重度污染	严重污染
AQI值范围	[0,50）	[50，100）	[100,150）	[150,200）	[200,300）	300及以上

 
下表是由天气网获得的全国东西部各6个城市2015年3月某时刻实时监测到的数据：

西部城市	AQI数值	东部城市	AQI数值
西安	108	北京	104
西宁	92	金门	42
克拉玛依	37	上海	x
鄂尔多斯	56	苏州	114
巴彦淖尔	61	天津	105
库尔勒	456	石家庄	93
AQI平均值：135	AQI平均值：90

 
（Ⅰ）求x的值，并根据上表中的统计数据，判断东、西部城市AQI数值的方差的大小关系（只需写出结果）；
（Ⅱ）环保部门从空气质量“优”和“轻度污染”的两类城市随机选取个城市组织专家进行调研，记选到空气质量“轻度污染”的城市个数为，求的分布列和数学期望．

投到某杂志的稿件，先由两位初审专家进行评审．若能通过两位初审专家的评审，则予以录用；若两位初审专家都未予通过，则不予录用；若恰能通过一位初审专家的评
审，则再由第三位专家进行复审，若能通过复审专家的评审，则予以录用，否则不予录用．设稿件能通过各初审专家评审的概率均为 $0.5$，复审的稿件能通过评审的概率为 $0.3$．各专家独立评审．
（I）求投到该杂志的1篇稿件被录用的概率；
（II）记 $X$表示投到该杂志的4篇稿件中被录用的篇数，求 $X$的分布列及期望．

(本小题满分12分) 甲、乙、丙三人按下面的规则进行乒乓球比赛: 第一局由甲、乙参加而丙轮空，以后每一局由前一局的获胜者与轮空者进行比赛，而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或打满6局时停止.设在每局中参赛者胜负的概率均为，且各局胜负相互独立.
求：（I）打满3局比赛还未停止的概率；
（II）比赛停止时已打局数的分别列与期望E.

第16届亚运会将于2010年11月12日至27日在中国广州进行，在安全保障方面，警方从武警训练基地挑选防爆警察，从体能、射击、反应三项指标进行检测，如果这三项中至少有两项通过即可入选。假定某基地有4名武警战士（分别记为A、B、C、D）拟参加挑选，且每人能通过体能、射击、反应的概率分别为。这三项测试能否通过相互之间没有影响。试卷
（1）求A能够入选的概率；试卷                                                                                                                                                                                                                                                                                                                                                                  
（2）规定：按人选人数得训练经费（每人选1人，则相应的训练基地得到3000元的训练经费），求该基地得到训练经费的分布列与数学期望。

某次有奖竞猜活动设有、两组相互独立的问题，答对问题可赢得奖金3000元，答对问题可赢得奖金6000元．规定答题顺序可任选，但只有一个问题答对后才能解答下一个问题，否则中止答题，假设你答对问题、的概率依次为．
（Ⅰ）若你按先后的次序答题，写出你获得奖金的数额的分布列及期望；
（Ⅱ）你认为获得奖金期望的大小与答题顺序有关吗？证明你的结论．

（本题12分）某种家电器每台的销售利润与该电器无故障使用时间T（单位：年）有关，若T≤1，则销售利润为0元，若1＜T≤3，则销售利润为100元，若T＞3，则销售利润为200元，设每台该种电台无故障使用时间T≤1，1＜T≤3及T＞3这三种情况发生的概率为为P₁，P₂，P₃，又知P₁，P₂是方程25x²－15x＋a＝0的两个根，且P₂＝P₃，
（1）求P₁，P₂，P₃的值；
（2）记表示销售两台这种家用电器的销售利润总和，求的分布列；
（3）求销售两台这种家用电器的销售利润总和的平均值。

某校高一年级有四个班，其中一、二班为数学课改班，三、四班为数学非课改班．在期末考试中，课改班与非课改班的数学成绩优秀与非优秀人数统计如表．

	优秀	非优秀	总计
课改班		50
非课改班	20		110
合计			210

（1）请完成上面的2×2列联表，并判断若按99%的可靠性要求，能否认为“成绩与课改有关”；
（2）把全部210人进行编号，从编号中有放回抽取4次，每次抽取1个，记被抽取的4人中的优秀人数为ξ，若每次抽取的结果是相互独立的，求ξ的分布列及数学期望Eξ．

（本小题满分12分）
某班级甲组有名学生，其中有名女生；乙组有名学生，其中有名女生.
（Ⅰ）若从两组中各抽取两人进行心理健康测试，求每组至少抽到一名女生的概率；
（Ⅱ）现采用分层抽样方法（层内采用不放回简单随机抽样）从甲、乙两组中共抽
取名学生进行心理健康测试.
（）求从甲、乙两组各抽取的人数；
（）记表示抽取的名学生中男生人数，求的分布列及数学期望.

（本小题10分）口袋中有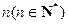个白球，3个红球．依次从口袋中任取一球，如果取到红球，那么继续取球，且取出的红球不放回；如果取到白球，就停止取球．记取球的次数为X．若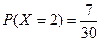，求：
（1）n的值；
（2）X的概率分布与数学期望．

已知正方形的边长为，、、、分别是边、、、的中点．
（1）在正方形内部随机取一点，求满足的概率；
（2）从、、、、、、、这八个点中，随机选取两个点，记这两个点之间的距离的平方为，求随机变量的分布列与数学期望．

(本小题满分12分)
某单位举办2010年上海世博会知识宣传活动，进行现场抽奖．盒中装有9张大小相同的精美卡片，卡片上分别印有“世博会会徽”或“海宝”(世博会吉祥物)图案；抽奖规则是：参加者从盒中抽取卡片两张，若抽到两张都是“海宝”卡即可获奖，否则，均为不获奖．卡片用后放回盒子，下一位参加者继续重复进行．
(Ⅰ)活动开始后，一位参加者问：盒中有几张“海宝”卡?主持人答：我只知道，从盒中抽取两张都是“世博会会徽”卡的概率是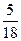，求抽奖者获奖的概率；
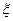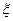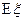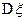(Ⅱ)现有甲乙丙丁四人依次抽奖，用表示获奖的人数，求的分布列及，的值．

为了更好地服务于2010年世博会，上海某酒店随机地对最近入住的名旅客进行服务质量问卷调查，把旅客对住宿的舒适满意度与价格满意度分为五个等级：
“1级（很不满意）”、“2级（不满意）”、“3级（一般）”、“4级（满意）”、“5级（很满意）”其结果如表所示，若在这个样本中，任选一人，其舒适度为，价格满意度.

(1)根据样本中的数据求P（y=5）及P（x≥3且y=3）的值；
(2)若的期望值为，求a、b、c的值；
(3)求该人在对价格满意（满意度不低于3）的条件下对舒适度也满意的概率.

上海世博会上有一种舞台灯，外形是正六棱柱，在其每个侧面（编号分别是①②③④⑤⑥）上安装5只颜色各异的灯，每只灯正常发光的概率是0.5，若一侧面上至少有3只灯发光，则不需要更换这个面，否则需要更换这个面，假定更换一个面需要100元，用表示更换费用。
（1）求①号面需要更换的概率；
（2）求6个侧面面上恰有2个侧面需要更换的概率。
（3）写出的分布列，并求出的数学期望。