高中数学二次剩余试题

若一元二次不等式对一切实数都成立，则的取值范围为（  ）

A．

B．

C．

D．

已知函数f(x)=x²-2x+3在闭区间［0,m］上最大值为3，最小值为2，则m的取值范围为           

在直角坐标系中，曲线C₁的参数方程为：（为参数），以原点为极点，x轴的正半轴为极轴，并取与直角坐标系相同的长度单位，建立极坐标系，曲线C₂是极坐标方程为：，
（1）求曲线C₂的直角坐标方程；
（2）若P，Q分别是曲线C₁和C₂上的任意一点，求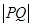的最小值.

对一切实数，所有的二次函数的值均为非负实数，则的最大值是____________．

已知
（1）设，求的最大值与最小值；
（2）求的最大值与最小值；

已知函数（为实常数）．
（1）若，求函数的单调区间；
（2）设在区间上的最小值为，求的表达式．

对于任意a∈[-1,1],函数f(x)=x²+(a-4)x+4-2a的值恒大于零,那么x的取值范围是(　　)

A．(1,3)	B．(-∞,1)∪(3,+∞)
C．(1,2)	D．(3,+∞)

（本小题满分10分）已知函数f（x）＝x²＋ax＋b的图象关于直线x＝1对称．
（1）求实数a的值
（2）若f（x）的图象过（2，0）点，求x∈[0，3]时f（x）的值域．

设函数f(x)＝ax－(1＋a²)x²，其中a>0，区间I＝{x|f(x)>0}．
(1)求I的长度(注：区间(α，β)的长度定义为β－α)；
(2)给定常数k∈(0，1)，当1－k≤a≤1＋k时，求I的长度的最小值．

已知函数，若存在实数、、、，满足 ，其中，则的取值范围是           .

A．

B．

C．

D．

（1）已知，求的最小值；
（2）已知，求的最大值．

已知函数，其中．
（1）若，且的最大值为，最小值为，试求函数的最小值；
（2）若对任意实数，不等式恒成立，且存在使得成立，求的值；
（3）对于问（1）中的，若对任意的，恒有，求的取值范围．

（本小题满分14分）设二次函数满足下列条件：
①当时，其最小值为0，且成立；
②当时，恒成立．
（1）求的值；
（2）求的解析式；
（3）求最大的实数,使得存在，只要当时，就有成立

若关于的不等式的解集中有且仅有4个整数解，则实数的取值范围是     ．

一次函数是上的增函数，,已知.
（1）求；
（2）若在单调递增，求实数的取值范围；
（3）当时，有最大值，求实数的值.