高中数学二次剩余选择题

已知函数，若存在实数、、、，满足 ，其中，则的取值范围是           .

A．

B．

C．

D．

已知函数f(x)＝x²－2(a＋2)x＋a²，g(x)＝－x²＋2(a－2)x－a²＋8.设H₁(x)＝max{f(x)，g(x)}，H₂(x)＝min{f(x)，g(x)}(max{p，q}表示p，q中的较大值，min{p，q}表示p，q中的较小值)．记H₁(x)的最小值为A，H₂(x)的最大值为B，则A－B＝(　　)

A．a^2－2a－16

B．a^2＋2a－16

C．－16

D．16

若在区间(-∞，1]上递减，则a的取值范围为(    )

A．[1，2)

B．[1，2]

C．[1,+∞)

D．[2，+∞)

已知直线y＝mx与函数的图象恰好有3个不同的公共点，则实数m的取值范围是（   ）

A．(，4)

B．(，＋∞)

C．(，5)

D．(，)

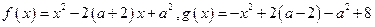已知函数．设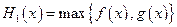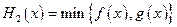， (max{p，q}表示p，q中的较大值，min{p，q}表示p，q中的较小值)．记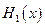的最小值为A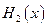，的最大值为B，则(    )

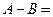A．16

B．

C．

D．

若一元二次不等式对一切实数都成立，则的取值范围为（  ）

A．

B．

C．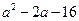

D．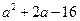

对于任意a∈[-1,1],函数f(x)=x²+(a-4)x+4-2a的值恒大于零,那么x的取值范围是(　　)

A．(1,3)	B．(-∞,1)∪(3,+∞)
C．(1,2)	D．(3,+∞)

．定义域为R的函数满足，且当时，，则当时，的最小值为（   ）

A．

B．

C．

D．

若函数有两个零点，其中，那么在两个函数值中   (    )

A．只有一个小于1	B．至少有一个小于1
C．都小于1	D．可能都大于1

设 $f\left(x\right)=\left\{\begin{array}{l}{x}^2,\left|x\ge 1\right|\\ x,\left|x\right|<1\end{array}\right.$, $g\left(x\right)$是二次函数，若 $f\left(g\right(x\left)\right)$的值域是 $[0,+\infty )$，则 $g\left(x\right)$的值域是（   ）

A．	$(-\infty ,-1][1,+\infty )$	B．	$(-\infty ,-1][0,+\infty )$
C．	$[0,+\infty )$	D．	$[1,+\infty )$

已知是偶函数，则函数图象与轴交点的纵坐标的最大值是（    ）

A．

B．2

C．

D．4