函数f(x)=x2-3x+2的零点是( )
A. 或 或 |
B. 或 或 |
| C.1或2 | D.-1或-2 |
已知函数y=4x-3×2x+3,当其值域为[1,7]时,则变量x的取值范围是
| A.[2,4] | B.(-∞,0] |
| C.(0,1]∪[2,4] | D.(-∞,0]∪[1,2] |
已知函数f(x)=x2+2x+alnx,若函数f(x)在(0,1)上单调,则实数a的取值范围是( )
| A.a≥0 | B.a<-4 | C.a≥0或a≤-4 | D.a>0或a<-4 |
已知函数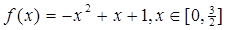 的最值情况为( )
的最值情况为( )
A.有最小值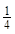 ,有最大值1 ,有最大值1 |
B.有最小值 ,有最大值 ,有最大值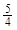 |
C.有最小值1,有最大值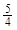 |
D.有最小值,无最大值 |
若函数 为偶函数,且函数
为偶函数,且函数 在
在 上单调递增,则实数
上单调递增,则实数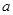 的值为( )
的值为( )
A. |
B.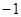 |
C. |
D. |
试题篮
()