高中数学二次剩余解答题

（1）已知是一次函数，且满足，求的解析式；
（2）已知函数满足，求的解析式。

定义区间的区间长度为，如图是某圆拱形桥一孔圆拱的示意图．这个圆的圆拱跨度，拱高，建造时每间隔需要用一根支柱支撑，求支柱的高度所处的区间．（要求区间长度为）

已知函数f（x）=x²+2ax+2，x∈[﹣5，5]．
（1）当a=﹣1时，求函数的最大值和最小值；
（2）求实数a的取值范围，使y=f（x）在区间[﹣5，5]上是单调函数．

（本小题满分10分）函数f（x）＝4x²－4ax＋a²－2a＋2在区间[0,2]上有最小值3，求a的值．

当﹣2≤x≤1时，二次函数有最大值4，求实数m取值的集合．

已知二次函数，当时，函数取最小值，且．
（1）求的解析式；
（2）若在区间上不单调，求实数的取值范围．

函数在闭区间上的最小值记为
（1）求的函数表达式；
（2）作的图像，并写出的最小值．

对于函数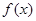，若在定义域内存在实数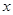，满足，则称为“局部奇函数”
（1）已知二次函数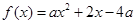（且），试判断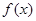是否为“局部奇函数”，并说明理由；
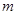（2）若是定义在区间上的“局部奇函数”，求实数的取值范围；
（3）若为定义域为上的“局部奇函数”，求实数的取值范围；

设二次函数 (,)，
满足条件：①当时，，且；
②当时，；
③f(x)在R上的最小值为0.
求最大值m()，使得存在，只要，就有.

若二次函数满足，且．
（1）求的解析式；
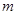（2）若在区间上，不等式恒成立，求实数的取值范围．

已知函数f（x）=x²+2x+alnx（a∈R）．
（1）当时a=﹣4时，求f（x）的最小值；
（2）若函数f（x）在区间（0，1）上为单调函数，求实数a的取值范围．

二次函数的图像顶点为，且图象在轴上截得线段长为．
（1）求函数的解析式；
（2）令
①若函数在上是单调增函数，求实数的取值范围；
②求函数在的最小值．

已知函数，
（1）求在区间的最小值；（2）求在区间的值域

已知二次函数满足．
（1）求的解析式；
（2）若在上有最小值，最大值，求a的取值集合．

（本小题满分14分）函数和的图象的示意图如图所示，设两函数的图象交于点 ，，且．

（1）请指出示意图中曲线，分别对应哪一个函数?
（2）证明：，且；
（3）结合函数图象的示意图，判断，，，的大小，并按从小到大的顺序排列．