高中数学第二数学归纳法解答题

已知f(n)＝1＋n∈N^)，g(n)＝2(－1)(n∈N^)．
(1)当n＝1，2，3时，分别比较f(n)与g(n)的大小(直接给出结论)；
(2)由(1)猜想f(n)与g(n)的大小关系，并证明你的结论．

数列满足．
（1）计算，，，，并由此猜想通项公式；
（2）用数学归纳法证明（1）中的猜想．

设n∈N^*，f(n)＝1＋＋＋…＋，试比较f(n)与的大小．

在数列中，已知，且。
（1）用数学归纳法证明：；
（2）求证．

用数学归纳法证明对n∈N_＋都有.

在数列中，，且. 求，猜想的表达式，并加以证明.

已知函数f(x)=x³-x,数列{a_n}满足条件:a₁≥1,a_n+1≥f'(a_n+1).试比较+++…+与1的大小,并说明理由.

【原创】
（1）观察下列各式;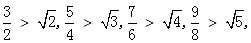根据以上各式利用归纳推理得出一个一般性的结论；
（2）设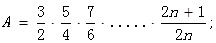根据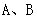的大小关系证明（1）的结论；

用数学归纳法证明:++…+= (n∈N^*).

已知数列的前n项和为，且，令.
（1）求证：数列是等差数列，并求数列的通项公式；
（2）若，用数学归纳法证明是18的倍数．

设函数其中是的导函数．
（1）令，猜测的表达式并给予证明；
（2）若恒成立，求实数的取值范围；
（3）设，比较与的大小，并说明理由．

已知函数，数列满足，．
（1）求；
（2）猜想数列的通项，并用数学归纳法予以证明．

(本小题满分12分)
已知数列满足，.
（1）计算，，，的值；
（2）根据以上计算结果猜想的通项公式，并用数学归纳法证明你的猜想.

观察下列各不等式：




…
（1）由上述不等式，归纳出一个与正整数有关的一般性结论；
（2）用数学归纳法证明你得到的结论．

是否存在常数使得对一切恒成立？若存在，求出的值，并用数学归纳法证明；若不存在，说明理由.