已知角A、B、C为△ABC的三个内角,其对边分别为a、b、c,若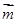 =(-cos
=(-cos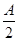 ,sin
,sin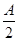 ),
),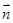 =(cos
=(cos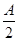 ,sin
,sin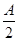 ),a=2
),a=2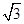 ,且
,且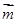 ·
·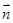 =
=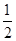 .
.
(1)若△ABC的面积S=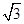 ,求b+c的值.
,求b+c的值.
(2)求b+c的取值范围.
设△ABC三个内角A、B、C所对的边分别为a,b,c. 已知C= ,acosA=bcosB.
,acosA=bcosB.
(1)求角A的大小;
(2)如图,在△ABC的外角∠ACD内取一点P,使得PC=2.过点P分别作直线CA、CD的垂线PM、PN,垂足分别是M、N.设∠PCA=α,求PM+PN的最大值及此时α的取值.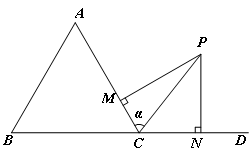
在 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为 、
、 、
、 ,已知向量
,已知向量 、
、 ,且
,且 .
.
(1)求角 的大小;
的大小;
(2)若 ,求
,求 面积的最大值.
面积的最大值.
在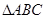 中,角
中,角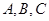 所对的边分别为
所对的边分别为 ,且满足
,且满足 .
.
(1) 求角 的大小;
的大小;
(2) 当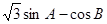 取得最大值时,请判断
取得最大值时,请判断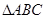 的形状.
的形状.
已知向量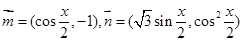 ,设函数
,设函数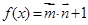
(1)求函数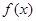 的单调递增区间;
的单调递增区间;
(2)在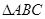 中,角
中,角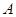 、
、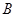 、
、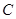 的对边分别为
的对边分别为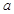 、
、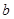 、
、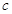 ,且满足
,且满足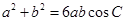 ,
,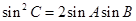 ,求
,求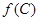 的值.
的值.
△ABC中,角A,B,C的对边分别为a,b,c,已知sinAsinB+sinBsinC+cos2B=1.
(1)求证:a,b,c成等差数列;(2)若C=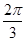
 ,求
,求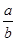 的值.
的值.
在△ 中,角
中,角 、
、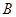 、
、 所对的边分别为
所对的边分别为 、
、 、
、 ,已知
,已知 (
( ),且
),且 .
.
(1)当 ,
, 时,求
时,求 ,
, 的值;
的值;
(2)若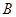 为锐角,求实数
为锐角,求实数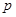 的取值范围.
的取值范围.
在直三棱柱ABC-A1B1C1中,已知AB=5,AC=4,BC=3,AA1=4,点D在棱AB上.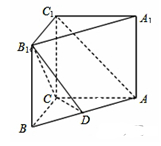
(1)若D是AB中点,求证:AC1∥平面B1CD;
(2)当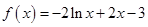 时,求二面角
时,求二面角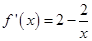 的余弦值.
的余弦值.
如图所示,扇形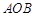 ,圆心角
,圆心角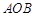 的大小等于
的大小等于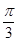 ,半径为2,在半径
,半径为2,在半径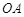 上有一动点
上有一动点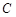 ,过点
,过点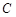 作平行于
作平行于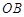 的直线交弧
的直线交弧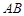 于点
于点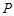 .
.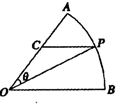
(1)若 是半径
是半径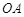 的中点,求线段
的中点,求线段 的长;
的长;
(2)设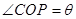 ,求
,求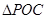 面积的最大值及此时
面积的最大值及此时 的值.
的值.
已知甲船正在大海上航行,当它位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待营救,甲船立即以10海里/小时的速度匀速前往救援,同时把消息告知在甲船的南偏西 ,相距10海里C处的乙船,乙船当即决定匀速前往救援,并且与甲船同时到达。(供参考使用:
,相距10海里C处的乙船,乙船当即决定匀速前往救援,并且与甲船同时到达。(供参考使用: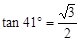 ).
).
(1)试问乙船航行速度的大小;
(2)试问乙船航行的方向(试用方位角表示,如北偏东…度).
设函数 .
.
(1)求 的最小正周期和值域;
的最小正周期和值域;
(2)在锐角△ 中,角
中,角 的对边分别为
的对边分别为 ,若
,若 且
且 ,
, ,求
,求 和
和 .
.
试题篮
()