在 中,
中,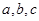 分别是内角
分别是内角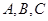 的对边,且
的对边,且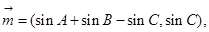
 ,且
,且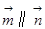 .
.
(1)求角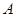 的大小;
的大小;
(2)若 边上高为1,求
边上高为1,求 面积的最小值.
面积的最小值.
已知m=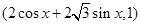 ,n=
,n= ,满足
,满足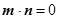 .
.
(1)将y表示为x的函数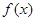 ,并求
,并求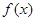 的最小正周期;
的最小正周期;
(2)已知a,b,c分别为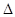 ABC的三个内角A,B,C对应的边长,
ABC的三个内角A,B,C对应的边长,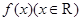 的最大值是
的最大值是 ,且a=2,求b+c的取值范围.
,且a=2,求b+c的取值范围.
已知函数 .
.
(1)若 ,求
,求 的取值范围;
的取值范围;
(2)设△ 的内角A、B、C所对的边分别为a、b、c,已知
的内角A、B、C所对的边分别为a、b、c,已知 为锐角,
为锐角, ,
, ,
, ,求
,求 的值.
的值.
已知函数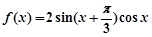 .
.
(1)若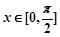 ,求
,求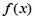 的取值范围;
的取值范围;
(2)设△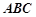 的内角A、B、C所对的边分别为a、b、c,已知
的内角A、B、C所对的边分别为a、b、c,已知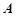 为锐角,
为锐角,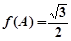 ,
,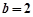 ,
,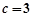 ,求
,求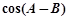 的值.
的值.
己知函数 在
在 处取最小值.
处取最小值.
(1)求 的值。
的值。
(2)在△ABC中,a、b、c分别是A、B、C的对边,已知a=l,b= ,
, ,求角C.
,求角C.
在海岸A处,发现北偏东45°方向、距离A处( -1)海里的B处有一艘走私船;在A处北偏西75°方向、距离A处2海里的C处的缉私船奉命以10
-1)海里的B处有一艘走私船;在A处北偏西75°方向、距离A处2海里的C处的缉私船奉命以10 海里/小时的速度追截走私船.同时,走私船正以10海里/小时的速度从B处向北偏东30°方向逃窜,问缉私船沿什么方向能最快追上走私船?最少要花多少时间?
海里/小时的速度追截走私船.同时,走私船正以10海里/小时的速度从B处向北偏东30°方向逃窜,问缉私船沿什么方向能最快追上走私船?最少要花多少时间?
设锐角三角形ABC的内角A,B,C的对边分别为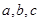 ,且
,且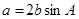 .
.
(1)求角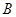 的大小;
的大小;
(2)若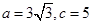 ,求
,求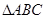 的面积及
的面积及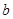 .
.
如图,在等腰直角△OPQ中,∠POQ=90°,OP=2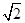 ,点M在线段PQ上.
,点M在线段PQ上.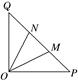
(1)若OM=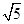 ,求PM的长;
,求PM的长;
(2)若点N在线段MQ上,且∠MON=30°,问:当∠POM取何值时,△OMN的面积最小?并求出面积的最小值.
在△ABC中,角A,B,C的对边分别为a,b,c,若acos2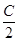 +ccos2
+ccos2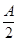 =
=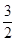 b.
b.
(1)求证:a,b,c成等差数列;
(2)若∠B=60°,b=4,求△ABC的面积.
如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50 m/min.在甲出发2 min后,乙从A乘缆车到B,在B处停留1 min后,再从B匀速步行到C.假设缆车匀速直线运动的速度为130 m/min,山路AC长为1 260 m,经测量cos A=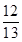 ,cos C=
,cos C= .
.
(1)求索道AB的长;
(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短?
(3)为使两位游客在C处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?
试题篮
()