高中数学三面角、直三面角的基本性质解答题

（本小题满分14分）
已知函数为R上的奇函数
(1)求的值
(2)求函数的值域
（3）判断函数的单调区间并证明

已知函数是上的奇函数，当时，，
（1）判断并证明在上的单调性；
（2）求的值域； 
（3）求不等式的解集。

设函数，求并求的值

（本小题满分14分）已知函数，，
，其中且.
（I）求函数的导函数的最小值；
（II）当时，求函数的单调区间及极值；
（III）若对任意的，函数满足，求实数
的取值范围.

（本题满分14分
某工厂生产一种产品的成本费由三部分组成
①职工工资固定支出元
②原材料费每件40元
③电力与机器保养等费用为每件元，其中是该厂生产这种产品的总件数.
（1）把每件产品的成本费（元）表示成产品件数的函数，并求每件产品的最低成本费；
（2）如果该厂生产的这种产品的数量不超过件，且产品能全部销售．根据市场调查：每件产品的销售价与产品件数有如下关系：，试问生产多少件产品，总利润最高？（总利润=总销售额—总的成本）

（本小题满分12分）自然状态下的鱼类是一种可再生的资源，为了持续利用这一资源，需从宏观上考察其再生能力及捕捞强度对鱼群总量的影响。用表示某鱼群在第年初的总量，，且。不考虑其他因素，设在第年内鱼群的繁殖量及被捕捞量都与成正比，死亡量与成正比，这些比例系数依次为正数其中称为捕捞强度。
（1）求与的关系式；
（2）设，为了保证对任意，都有，则捕捞强度的最大允许值是多少？证明你的结论。

(本小题满分12分）
（1） 化简 
（2.）若函数的定义域为[-1，1]，求函数+的定义域

(本小题满分12分)（1）对于定义在上的函数，满足，求证：函数在上是减函数；
（2）请你认真研读（1）中命题并联系以下命题：若是定义在上的可导函数，满足，则是上的减函数。然后填空建立一个普遍化的命题：
设是定义在上的可导函数，，若   +，
则        是上的减函数。
注：命题的普遍化就是从考虑一个对象过渡到考虑包含该对象的一个集合；或者从考虑一个较小的集合过渡到考虑包含该较小集合的更大集合。
（3）证明（2）中建立的普遍化命题。

已知函数，设。
（Ⅰ）求F（x）的单调区间；
（Ⅱ）若以）图象上任意一点为切点的切线的斜率 恒
成立，求实数的最小值。
（Ⅲ）是否存在实数，使得函数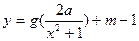的图象与的图象恰
好有四个不同的交点？若存在，求出的取值范围，若不存在，说明理由。来

设 $a>0,b>0$，已知函数 $f\left(x\right)=\frac{ax+b}{x+1}$．
（Ⅰ）当 $a\ne b$时，讨论函数 $f\left(x\right)$的单调性；
（Ⅱ）当 $x>0$时，称 $f\left(x\right)$为 $a,b$关于 $x$的加权平均数．
（1）判断 $f\left(1\right),f\left(\sqrt{\frac{b}{a}}\right),f\left(\frac{b}{a}\right)$是否成等比数列，并证明 $f\left(\frac{b}{a}\right)\le f\left(\sqrt{\frac{b}{a}}\right)$；
（2） $a,b$的几何平均数记为 $G$．称 $\frac{2ab}{a+b}$为 $a,b$的调和平均数，记为 $H$．若 $H\le f\left(x\right)\le G$，求 $x$的取值范围．

（本小题满分12分）已知函数
（1）若对一切实数x恒成立，求实数a的取值范围。
（2）求在区间上的最小值的表达式。

已知函数将的图象向右平移2个单位，得到的图象．
（1）求函数的解析式；
(2) 若函数与函数的图象关于直线对称，求函数的解析式；
(3)设已知的最小值是，且求实数的取值范围．

（本小题满分15分）已知函数，
（Ⅰ）判断函数的奇偶性；
（Ⅱ）求函数的单调区间；
（Ⅲ）若关于的方程在上有实数解，求实数的取值范围．

（本小题满分16分）
设，，函数
（1）设不等式的解集为C，当时，求实数取值范围
（2）若对任意，都有成立，试求时，的值域
（3）设 ，求的最小值

（本小题满分12分）养路处建造圆锥形仓库用于贮藏食盐（供融化高速公路上的积雪之用）.已建仓库的底面直径为12m,高4m.养路处拟建一个更大的圆锥形仓库，以存放更多食盐，现有两种方案：一是新建的仓库的底面直径比原来大4m(高不变)；二是高度增加4m（底面直径不变）.
（1）分别计算按这两种方案所建的仓库的体积；
（2）分别计算按这两种方案所建的仓库的表面积（底面面积不计）；
（3）哪个方案更经济些？