高中数学三面角、直三面角的基本性质试题

已知函数f(x)＝|x＋1|，g(x)＝2|x|＋a.
(1)当a＝0时，解不等式f(x)≥g(x)；
(2)若任意x∈R，f(x)g(x)恒成立，求实数a的取值范围．

设函数，．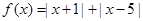
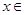
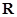⑴ 求不等式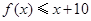的解集；
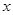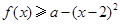⑵ 如果关于的不等式在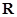上恒成立，求实数的取值范围．

已知函数f(x)＝ (a、b为常数)，且方程f(x)－x＋12＝0有两个实根为x₁＝3，x₂＝4.
(1)求函数f(x)的解析式；
(2)设k>1，解关于x的不等式f(x)< .

定义在上的偶函数，对任意实数都有，当时，，若在区间内，函数与函数的图象恰有4个交点，则实数的取值范围是__________.

点A(a＋b，ab)在第一象限内，则直线bx＋ay－ab＝0不经过的象限是(　　)

A．第一象限

B．第二象限

C．第三象限

D．第四象限

为了在夏季降温和冬季供暖时减少能源损耗，房屋的房顶和外墙需要建造隔热层，某幢建筑物要建造可使用20年的隔热层，每厘米厚的隔热层建造成本为6万元，该建筑物每年的能源消耗费用为C（单位：万元）与隔热层厚度x（单位：cm）满足关系：C（x）=（0x10），若不建隔热层，每年能源消耗费用为8万元。设f（x）为隔热层建造费用与20年的能源消耗费用之和。
(1)求k的值及f(x)的表达式；
(2)隔热层修建多厚时，总费用f（x）达到最小，并求最小值。

已知函数,若f(x)在x=1处的切线方程为3x+y-6=0
（Ⅰ）求函数f(x)的解析式;
（Ⅱ）若对任意的,都有f(x)成立,求函数g(t)的最值

函数的定义域为D，若存在闭区间[a，b]D，使得函数满足：
(1) 在[a，b]内是单调函数；
(2)在[a，b]上的值域为[2a，2b]，则称区间[a，b]为y=的“和谐区间”．
下列函数中存在“和谐区间”的是            (只需填符合题意的函数序号).
①；②；③；④.

函数恒过定点________  ____.

如图，公园有一块边长为2的等边△ABC的边角地，现修成草坪，图中把草坪分成面积相等的两部分，在上，在上.

（1）设，求用表示的函数关系式；
（2）如果是灌溉水管，为节约成本，希望它最短，的位置应在哪里？如果是参观线路，则希望它最长，的位置又应在哪里？请说明理由.

已知函数在处取得极小值.
(1)求的值；
(2)若在处的切线方程为，求证：当时，曲线不可能在直线的下方.

已知m∈R，对p：x₁和x₂是方程x²－ax－2＝0的两个根，不等式|m－5|≤|x₁－x₂|对任意实数a∈[1,2]恒成立；q：函数f(x)＝3x²＋2mx＋m＋有两个不同的零点.求使“p且q”为假命题、“p或q”为真命题的实数m的取值范围．

设函数，且曲线斜率最小的切线与直线平行.求：（1）的值；(2）函数的单调区间.

设奇函数的定义域为Ｒ，最小正周期，若，则的取值范围是

A．	B．
C．	D．

设函数.
(1) 试问函数f(x)能否在x= 时取得极值？说明理由；
(2) 若a= ，当x∈［,4］时，函数f(x)与g(x)的图像有两个公共点，求c的取值范围.