给出下列四个命题, 其中正确的命题有
 个.
个.
(1)函数 上的单调递增区间是
上的单调递增区间是 ;
;
(2) 均为非零实数,集合
均为非零实数,集合 ,则“
,则“ ”是“
”是“ ”的必要不充分条件
”的必要不充分条件
(3)若 为真命题,则
为真命题,则 也为真命题
也为真命题
(4) 命题 的否定
的否定
A. |
B. |
C. |
D. |
若存在实常数 和
和 ,使得函数
,使得函数 和
和 对其公共定义域上的任意实数
对其公共定义域上的任意实数 都满足:
都满足: 和
和 恒成立,则称此直线
恒成立,则称此直线 为
为 和
和 的“隔离直线”.已知函数
的“隔离直线”.已知函数 .有下列命题:
.有下列命题:
① 在
在 内单调递增;
内单调递增;
② 和
和 之间存在“隔离直线”, 且b的最小值为-4;
之间存在“隔离直线”, 且b的最小值为-4;
③ 和
和 之间存在“隔离直线”, 且k的取值范围是
之间存在“隔离直线”, 且k的取值范围是 ;
;
④ 和
和 之间存在唯一的“隔离直线”
之间存在唯一的“隔离直线” .
.
其中真命题的个数有( ).
| A.1个 | B.2个 | C.3个 | D.4个 |
下列说法正确的是( )
A.命题“若 ,则 ,则 ”的逆命题是“若 ”的逆命题是“若 ,则 ,则 ” ” |
B.命题“若 ,则 ,则 ”的否命题是“若 ”的否命题是“若 ,则 ,则 ” ” |
C.已知 ,命题“若 ,命题“若 ,则 ,则 ”的逆否命题是真命题 ”的逆否命题是真命题 |
D.若 ,则“ ,则“ ”是“ ”是“ ”的充分条件 ”的充分条件 |
已知下列三个命题:
①棱长为2的正方体外接球的体积为4 ;
;
②如果将一组数据中的每一个数都加上同一个非零常数,那么这组数据的平均数和方差都改变;
③直线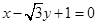 被圆
被圆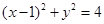 截得的弦长为2
截得的弦长为2 .
.
其中真命题的序号是( )。
| A.①② | B.②③ | C.①③ | D.①②③ |
下列说法中,不正确的是( )
A.已知 ,命题“若 ,命题“若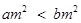 ,则 ,则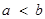 ”为真命题; ”为真命题; |
B.命题“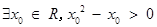 ”的否定是:“ ”的否定是:“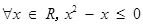 ”; ”; |
C.命题“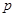 或 或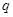 ”为真命题,则命题 ”为真命题,则命题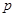 和命题 和命题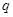 均为真命题; 均为真命题; |
D.“ ”是“ ”是“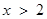 ”的充分不必要条件. ”的充分不必要条件. |
下列四个命题中,正确的有
①两个变量间的相关系数 越小,说明两变量间的线性相关程度越低;
越小,说明两变量间的线性相关程度越低;
②命题 :“
:“ ,
, ”的否定
”的否定 :“
:“ ,
, ”;
”;
③用相关指数 来刻画回归效果,若
来刻画回归效果,若 越大,则说明模型的拟合效果越好;
越大,则说明模型的拟合效果越好;
④若 ,
, ,
, ,则
,则 .
.
| A.①③④ | B.①④ | C.③④ | D.②③ |
下列命题正确的个数有( )
(1)命题“ 为真”是命题“
为真”是命题“ 为真”的必要不充分条件
为真”的必要不充分条件
(2)命题“ ,使得
,使得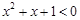 ”的否定是:“对
”的否定是:“对 ,均有
,均有 ”
”
(3)经过两个不同的点 、
、 的直线都可以用方程
的直线都可以用方程

 来表示
来表示
(4)在数列 中,
中, ,
,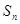 是其前
是其前 项和,且满足
项和,且满足 ,则
,则 是等比数列
是等比数列
(5)若函数 在
在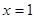 处有极值10,则
处有极值10,则
| A.1个 | B.2个 | C.3个 | D.4个 |
下面给出四个命题:
(1) 对于实数m和向量a、b恒有:m(a – b) =" ma" – mb;
(2) 对于实数m,n和向量a,恒有:(m – n)a =" ma" – na;
(3) 若ma =" mb" (m∈R,m¹0 ), 则a = b;
(4) 若ma =" na" (m,n∈R,a ≠ 0), 则m = n.
其中正确命题的个数是 ( )
| A.1 | B.2 | C.3 | D.4 |
下列说法中正确的是 ( )
A.“ ”是“函数 ”是“函数 是奇函数”的充要条件; 是奇函数”的充要条件; |
B.若 .则 .则 ; ; |
C.若 为假命题,则 为假命题,则 均为假命题; 均为假命题; |
D.“若 ,则 ,则 ”的否命题是“若 ”的否命题是“若 ,则 ,则 ”. ”. |
下列命题正确的个数有( )
(1)命题“ 为真”是命题“
为真”是命题“ 为真”的必要不充分条件
为真”的必要不充分条件
(2)命题“ ,使得
,使得 ”的否定是:“对
”的否定是:“对 , 均有
, 均有 ”
”
(3)经过两个不同的点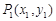 、
、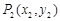 的直线都可以用方程
的直线都可以用方程

 来表示
来表示
(4)在数列 中,
中,  ,
,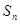 是其前
是其前 项和,且满足
项和,且满足 ,则
,则 是等比数列
是等比数列
(5)若函数 在
在 处有极值10,则
处有极值10,则
| A.1个 | B.2个 | C.3个 | D.4个 |
试题篮
()