已知:命题p:x1和x2是方程x2-mx-2=0的两个实根,且不等式a2-5a-3≥|x1-x2|对任意实数m∈[-1,1]恒成立;命题q:函数y=lg(ax2-x+a)的定义域为R.
若命题p是假命题,命题q是真命题,求a的取值范围.
给定下列结论:其中正确的个数是 ( )
①用20㎝长的铁丝折成的矩形最大面积是25㎝2;
②命题“所有的正方形都是矩形”的否定是“所有的正方形都不是矩形”;
③函数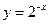 与函数
与函数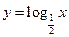 的图像关于直线
的图像关于直线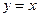 对称.
对称.
| A.0 | B.1 | C.2 | D.3 |
写出下列命题的否命题及命题的否定形式,并判断真假:
(1)若m>0,则关于x的方程x2+x-m=0有实数根;
(2)若x、y都是奇数,则x+y是奇数;
(3)若abc=0,则a、b、c中至少有一个为零.
指出下列命题的真假:
(1)命题“不等式(x+2)2≤0没有实数解”;
(2)命题“1是偶数或奇数”;
(3)命题“ 属于集合Q,也属于集合R”;
属于集合Q,也属于集合R”;
(4)命题“A A
A B”.
B”.
写出下列命题的否定并判断真假.
(1)p:所有末位数字是0的整数都能被5整除;
(2)q: x≥0,x2>0;
x≥0,x2>0;
(3)r:存在一个三角形,它的内角和大于180°;
(4)t:某些梯形的对角线互相平分.
分别指出由下列命题构成的“p q”、“p
q”、“p q”、“
q”、“ p”形式的命题的真假.
p”形式的命题的真假.
(1)p:4∈{2,3},q:2∈{2,3};
(2)p:1是奇数,q:1是质数;
(3)p:0∈ ,q:{x|x2-3x-5<0}
,q:{x|x2-3x-5<0} R;
R;
(4)p:5≤5,q:27不是质数;
(5)p:不等式x2+2x-8<0的解集是{x|-4<x<2},
q:不等式x2+2x-8<0的解集是{x|x<-4或x>2}.
已知两个命题r(x):sinx+cosx>m,s(x):x2+mx+1>0.如果对 x∈R,r(x)与s(x)有且仅有一个是真命题.求实数m的取值范围.
x∈R,r(x)与s(x)有且仅有一个是真命题.求实数m的取值范围.
写出下列命题的否命题,并判断原命题及否命题的真假:
(1)如果一个三角形的三条边都相等,那么这个三角形的三个角都相等;
(2)矩形的对角线互相平分且相等;
(3)相似三角形一定是全等三角形.
把下列命题改写成“若p,则q”的形式,并写出它们的逆命题、否命题、逆否命题.
(1)正三角形的三内角相等;
(2)全等三角形的面积相等;
(3)已知a,b,c,d是实数,若a=b,c=d,则a+c=b+d.
试题篮
()