德国著名数学家狄利克雷在数学领域成就显著,以其名命名的函数
被称为狄利克雷函数,其中 为实数集,
为实数集, 为有理数集,则关于函数
为有理数集,则关于函数 有如下四个命题:
有如下四个命题:
① ; ②函数
; ②函数 是偶函数;
是偶函数;
③任取一个不为零的有理数 ,
, 对任意的
对任意的 恒成立;
恒成立;
④存在三个点 ,使得
,使得 为等边三角形.
为等边三角形.
其中真命题的个数是( )
| A.1 | B.2 | C.3 | D.4 |
给出下列四个命题:
①命题“ ”的否定是“
”的否定是“ ”;
”;
②“ ”是“直线
”是“直线 与直线
与直线 相互垂直”的必要不充分条件;
相互垂直”的必要不充分条件;
③设圆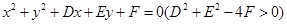 与坐标轴有4个交点,分别为
与坐标轴有4个交点,分别为 ,则
,则 ;
;
④关于 的不等式
的不等式 的解集为
的解集为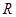 ,则
,则 .
.
其中所有真命题的序号是 .
下列命题正确的个数有( )
(1)命题“ 为真”是命题“
为真”是命题“ 为真”的必要不充分条件
为真”的必要不充分条件
(2)命题“ ,使得
,使得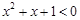 ”的否定是:“对
”的否定是:“对 ,均有
,均有 ”
”
(3)经过两个不同的点 、
、 的直线都可以用方程
的直线都可以用方程

 来表示
来表示
(4)在数列 中,
中, ,
,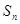 是其前
是其前 项和,且满足
项和,且满足 ,则
,则 是等比数列
是等比数列
(5)若函数 在
在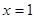 处有极值10,则
处有极值10,则
| A.1个 | B.2个 | C.3个 | D.4个 |
下列说法中,不正确的是( )
A.已知 ,命题“若 ,命题“若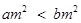 ,则 ,则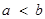 ”为真命题; ”为真命题; |
B.命题“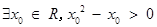 ”的否定是:“ ”的否定是:“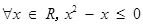 ”; ”; |
C.命题“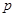 或 或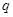 ”为真命题,则命题 ”为真命题,则命题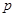 和命题 和命题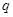 均为真命题; 均为真命题; |
D.“ ”是“ ”是“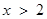 ”的充分不必要条件. ”的充分不必要条件. |
下列命题正确的个数有( )
(1)命题“ 为真”是命题“
为真”是命题“ 为真”的必要不充分条件
为真”的必要不充分条件
(2)命题“ ,使得
,使得 ”的否定是:“对
”的否定是:“对 , 均有
, 均有 ”
”
(3)经过两个不同的点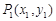 、
、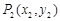 的直线都可以用方程
的直线都可以用方程

 来表示
来表示
(4)在数列 中,
中,  ,
,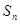 是其前
是其前 项和,且满足
项和,且满足 ,则
,则 是等比数列
是等比数列
(5)若函数 在
在 处有极值10,则
处有极值10,则
| A.1个 | B.2个 | C.3个 | D.4个 |
给出下列四个结论:
①命题“ 的否定是“
的否定是“ ”;
”;
②“若 则
则 ”的逆命题为真;
”的逆命题为真;
③函数 (x
(x )有3个零点;
)有3个零点;
④对于任意实数x,有 且x>0时,
且x>0时, 则x<0时
则x<0时
其中正确结论的序号是 .(填上所有正确结论的序号)
在下列给出的命题中,所有正确命题的序号为 .
①函数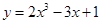 的图象关于点
的图象关于点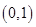 成中心对称;
成中心对称;
②对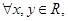 若
若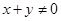 ,则
,则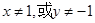 ;
;
③若实数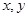 满足
满足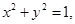 则
则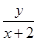 的最大值为
的最大值为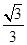 ;
;
④若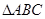 为钝角三角形,则
为钝角三角形,则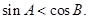
给出下列四个命题, 其中正确的命题有
 个.
个.
(1)函数 上的单调递增区间是
上的单调递增区间是 ;
;
(2) 均为非零实数,集合
均为非零实数,集合 ,则“
,则“ ”是“
”是“ ”的必要不充分条件
”的必要不充分条件
(3)若 为真命题,则
为真命题,则 也为真命题
也为真命题
(4) 命题 的否定
的否定
A. |
B. |
C. |
D. |
(本小题满分10分)设有两个命题: 关于x的不等式x2+2ax+4>0对一切x∈R恒成立;
关于x的不等式x2+2ax+4>0对一切x∈R恒成立; 函数f(x)=-(4-2a)x在(-∞,+∞)上是减函数.若命题
函数f(x)=-(4-2a)x在(-∞,+∞)上是减函数.若命题 为真,
为真, 为假,则实数a的取值范围是多少?
为假,则实数a的取值范围是多少?
已知函数 的定义域为
的定义域为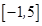 ,部分对应值如下表,
,部分对应值如下表, 的导函数
的导函数 的图象如图所示.下列关于
的图象如图所示.下列关于 的命题:
的命题:
 |
 |
0 |
4 |
5 |
 |
1 |
2 |
2 |
1 |
①函数 的极大值点为
的极大值点为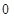 ,
, ;
;
②函数 在
在 上是减函数;
上是减函数;
③如果当 时,
时, 的最大值是2,那么
的最大值是2,那么 的最大值为4;
的最大值为4;
④当 时,函数
时,函数 有
有 个零点。
个零点。
其中正确命题的个数有 个.
试题篮
()