已知函数 (
( 为常数),其图象是曲线
为常数),其图象是曲线 .
.
(1)当 时,求函数
时,求函数 的单调减区间;
的单调减区间;
(2)设函数 的导函数为
的导函数为 ,若存在唯一的实数
,若存在唯一的实数 ,使得
,使得 与
与 同时成立,求实数
同时成立,求实数 的取值范围;
的取值范围;
(3)已知点 为曲线
为曲线 上的动点,在点
上的动点,在点 处作曲线
处作曲线 的切线
的切线 与曲线
与曲线 交于另一点
交于另一点 ,在点
,在点 处作曲线
处作曲线 的切线
的切线 ,设切线
,设切线 的斜率分别为
的斜率分别为 .问:是否存在常数
.问:是否存在常数 ,使得
,使得 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知数列 的前n项和为Sn,对一切正整数n,点
的前n项和为Sn,对一切正整数n,点 在函数
在函数 的图像上,且过点
的图像上,且过点 的切线的斜率为kn.
的切线的斜率为kn.
(1)求数列 的通项公式;
的通项公式;
(2)若 ,求数列
,求数列 的前n项和Tn.
的前n项和Tn.
已知P( )为函数
)为函数 图像上一点,O为坐标原点,记直线OP的斜率
图像上一点,O为坐标原点,记直线OP的斜率 。
。
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)设 ,求函数
,求函数 的最小值。
的最小值。
设函数 。
。
(Ⅰ)若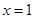 时,函数
时,函数 取得极值,求函数
取得极值,求函数 的图像在
的图像在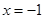 处的切线方程;
处的切线方程;
(Ⅱ)若函数 在区间
在区间 内不单调,求实数
内不单调,求实数 的取值范围。
的取值范围。
已知曲线 :
: .
.
(Ⅰ)当 时,求曲线
时,求曲线 的斜率为1的切线方程;
的斜率为1的切线方程;
(Ⅱ)设斜率为 的两条直线与曲线
的两条直线与曲线 相切于
相切于 两点,求证:
两点,求证: 中点
中点 在曲线
在曲线 上;
上;
(Ⅲ)在(Ⅱ)的条件下,又已知直线 的方程为:
的方程为: ,求
,求 的值.
的值.
在实数集R上定义运算:
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)若 在R上是减函数,求实数a的取值范围;
在R上是减函数,求实数a的取值范围;
(Ⅲ)若 ,在
,在 的曲线上是否存在两点,使得过这两点的切线互相垂直?若存在,求出切线方程;若不存在,说明理由.
的曲线上是否存在两点,使得过这两点的切线互相垂直?若存在,求出切线方程;若不存在,说明理由.
设函数 其中
其中 ,曲线
,曲线 在点
在点 处的切线方程为
处的切线方程为 .
.
(I)确定 的值;
的值;
(II)设曲线 在点
在点 处的切线都过点(0,2).证明:当
处的切线都过点(0,2).证明:当 时,
时, ;
;
(III)若过点(0,2)可作曲线 的三条不同切线,求
的三条不同切线,求 的取值范围.
的取值范围.
已知函数
(1)若函数 在点
在点 处的切线方程为
处的切线方程为 ,求
,求 的值;
的值;
(2)若 ,函数
,函数 在区间
在区间 内有唯一零点,求
内有唯一零点,求 的取值范围;
的取值范围;
(3)若对任意的 ,均有
,均有 ,求
,求 的取值范围.
的取值范围.
已知函数 ,且
,且 在
在 处的切线方程为
处的切线方程为 .
.
(1)求 的解析式;
的解析式;
(2)证明:当 时,恒有
时,恒有 ;
;
(3)证明:若 ,
, ,且
,且 ,则
,则 .
.
如下图,过曲线 :
: 上一点
上一点 作曲线
作曲线 的切线
的切线 交
交 轴于点
轴于点 ,又过
,又过 作
作  轴的垂线交曲线
轴的垂线交曲线 于点
于点 ,然后再过
,然后再过 作曲线
作曲线 的切线
的切线 交
交 轴于点
轴于点 ,又过
,又过 作
作 轴的垂线交曲线
轴的垂线交曲线 于点
于点 ,
, ,以此类推,过点
,以此类推,过点 的切线
的切线 与
与 轴相交于点
轴相交于点 ,再过点
,再过点 作
作 轴的垂线交曲线
轴的垂线交曲线 于点
于点 (
( N
N ).
).
(1) 求 、
、 及数列
及数列 的通项公式;(2) 设曲线
的通项公式;(2) 设曲线 与切线
与切线 及直线
及直线 所围成的图形面积为
所围成的图形面积为 ,求
,求 的表达式; (3) 在满足(2)的条件下, 若数列
的表达式; (3) 在满足(2)的条件下, 若数列 的前
的前 项和为
项和为 ,求证:
,求证:
 N
N .
.
(本小题满分14分)
已知函数 .
.
(1)求函数 的最小值;
的最小值;
(2)证明:对任意 恒成立;
恒成立;
(3)对于函数 图象上的不同两点
图象上的不同两点 ,如果在函数
,如果在函数 图象上存在点
图象上存在点 (其中
(其中 )使得点
)使得点 处的切线
处的切线 ,则称直线
,则称直线 存在“伴侣切线”.特别地,当
存在“伴侣切线”.特别地,当 时,又称直线
时,又称直线 存在 “中值伴侣切线”.试问:当
存在 “中值伴侣切线”.试问:当 时,对于函数
时,对于函数 图象上不同两点
图象上不同两点 、
、 ,直线
,直线 是否存在“中值伴侣切线”?证明你的结论.
是否存在“中值伴侣切线”?证明你的结论.
(本小题满分14分)已知函数 ,其中
,其中 .
.
(Ⅰ)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)当 时,求
时,求 的单调区间;
的单调区间;
(Ⅲ)证明:对任意的 在区间
在区间 内均存在零点.
内均存在零点.
试题篮
()