高中数学解答题

（本小题满分12分）已知向量。
（1）若f(x)=1，求cos(+x)的值；
（2）在△ABC中，角A、B、C的对边分别是a、b、c，且满足(2a-c)cosB=bcosC，
求函数f(A)的取值范围。

（本小题满分10分）某校从参加高一年级期中考试的学生中随机抽取60名学生，将其数学成绩(均为整数)分成六段[40, 50)，[50, 60)，…，[90, 100] 后得到如下部分频率分布直方图．观察图形的信息，回答下列问题：

（I）求分数在 [70，80)内的频率，并补全这个频率分布直方图；
（Ⅱ）统计方法中，同一组数据常用该组区间的中点值作为代表，据此估计本次考试的平均分；
(Ⅲ) 根据频率分布直方图估计这次高一年级期中考试的学生成绩的中位数(保留整数)。

求方程ax²＋2x＋1＝0有且只有一个负实数根的充要条件

指出下列各组命题中，p是q的什么条件？
(1)p：(x－2)(x－3)＝0；q：x－2＝0.
(2)p：四边形的对角线相等；q：四边形是平行四边形．
(3)p：m<－2，q：方程x²－x－m＝0无实根．

分别写出下列命题的逆命题、否命题、逆否命题，并判断它们的真假．
(1)若x、y都是奇数，则x＋y是偶数；
(2)若x>2，y>3，则x＋y>5.

若集合A＝{x|x²－2x－8＜0}，B＝{x|x－m＜0}．
(1)若m＝3，全集U＝A∪B，试求A∩(∁_UB)；
(2)若A∩B＝∅，求实数m的取值范围；
(3)若A∩B＝A，求实数m的取值范围．

已知集合A＝{x|x²－2x－3≤0，x∈R}，B＝{x|x²－2mx＋m²－4≤0，x∈R}．
(1)若A∩B＝[1,3]，求实数m的值；
(2)若A⊆∁_RB，求实数m的取值范围．

设集合A＝{x^2,2x－1，－4}，B＝{x－5,1－x,9}，若A∩B＝{9}，求A∪B.

设A={1,2,3,4}，B={1,2}，试求集合C，使C真包含于A且B包含于C

确定整数x,y，使{2x,x+y}={7,4}

如图，正方体ABCD－A₁B₁C₁D₁中，E，F分别为AB与BB₁的中点，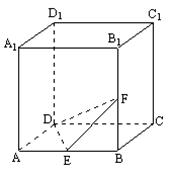

（Ⅰ）求证：EF⊥平面A₁D₁B ；
（Ⅱ）求二面角F－DE－C大小．

已知二次函数f(x)的二次项系数为a，且不等式f(x)>2x的解集为(-1，3)
(1)若方程f(x)=-7a有两个相等的实数根，求f(x)的解析式
(2)若函数f(x)在[-2，1]上的最大值为10，求a的值及f(x)在[-2，11]的最小值。

抛物线有光学性质：由其焦点射出的光线
经抛物线反象后，沿平行于抛物线对称轴的肖向射出，反之亦然。
如图所示，今有抛物线C，其顶点是坐标原点，对称辅为x轴。开
口向右。一光源在点M处，由其发出一条平行于x轴的光线射向
抛物线C卜的点P(4．4)，经抛物线C反射后，反射光线经过焦点
F后射向抛物线C上的点Q，再经抛物线C反射后又沿平行于X
轴的方向射出，途中经直线l：2x-4y-17=0上点N反射后又射回点M。
(1)求抛物线C的方程；
(2)求PQ的长度；
(3)判断四边形MPQN是否为平行四边形，若是请给出证明，若不是请说明理由。

设数列{a_n}的前n项和为Sn=2ⁿ⁺¹-2，{b_n }是公差不为0的等差数列，其中b₂、b₄、b₉依次成等比数列，且a₂=b₂
(1)求数列{a_n }和{b_n}的通项公式：
(2)设c_n=，求数列{c_n)的前n项和T_n

长方体ABCD-A₁B_lC_lD₁中，AB=2，AD=1，AA₁=，E、F分别是
AB、CD的中点
(1)求证：D_lE⊥平面AB_lF；
(2)求直线AB与平面AB_lF所成的角
(3)求二面角A-B₁F-B的大小。