高中数学解答题

（本小题满分10分）
设是一个公差为的等差数列，它的前10项和
且，，成等比数列,求公差的值和数列的通项公式.

(本小题满分8分)
临汾市染料厂生产化工原料，当年产量在150吨到250吨时，年生产总成本y（万元）与年产量x（吨）之间的关系可近似表示为,为使每吨平均成本最低，年产量指标应定在多少吨？（注：平均成本）

(本小题满分8分)
在△ABC中，若A=120°，AB=5，BC=，求△ABC的面积S.

(本小题满分10分)
已知各项均为正数的数列{a_n}前n项和为S_n，=2，且2，a_n，S_n成等差数列。

20070402

（1）求数列{a_n}的通项公式；

（2）若 ，求数列{ }的前n项和T_n；
（3）记数列 的前n项和为 ，求证： .

（本小题满分10分）
临汾市染料厂生产化工原料，当年产量在150吨到250吨时，年生产总成本
y（万元）与年产量x（吨）之间的关系可近似表示为
（1）为使每吨平均成本最低，年产量指标应定在多少吨？
（注：平均成本）
（2）若出厂价为每吨16万元，为获得最大的利润，年产量指标应定在多少吨，
并求出最大利润.

（本小题满分10分）
设是一个公差为的等差数列，它的前10项和且
，，成等比数列,求公差的值和数列的通项公式.

本小题满分8分）
已知锐角△ABC的三内角所对的边分别为，边a、b是方程
x²－2x+2=0的两根，角A、B满足关系2sin(A+B)－=0，求角C的度数，边c的长度及△ABC的面积.

（本小题满分8分）
已知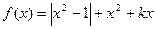关于的不等式的解集为，求关于的不等式的解集.

（本题12分）已知函数．
（1）若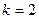，求函数的零点；
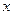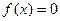（2）若关于的方程在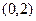上有2个不同的解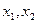，求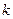的取值范围，并证明．

（本题12分）已知函数．
（1）当时，求函数的单调递减区间；
（2）当时，在上恒大于0，求实数的取值范围．

（本题8分）已知函数是奇函数，并且函数的图像经过点，
（1）求实数的值；
（2）求函数在时的值域．

（本题10分）如图所示，将一矩形花坛扩建成一个更大的矩形花坛，要求在的延长线上，在的延长线上，且对角线过点．已知米，米．
（1）设（单位：米），要使花坛的面积大于9平方米，求的取值范围；
（2）若（单位：米），则当，的长度分别是多少时，花坛的面积最大？并求出最大面积．

（本题8分）己知集合, 集合,
集合．
（1）求；
（2）若，求的取值范围．

如图，在三棱锥中，已知△是正三角形，平面，，为的中点，在棱上，且，
（1）求证：平面；
（2）求平面与平面所成的锐二面角的余弦值；
（3）若为的中点，问上是否存在一点，使平面？若存在，说明点的位置；若不存在，试说明理由．

如图，矩形与正三角形中， ，，为的中点。现将正三角形沿折起，得到四棱锥的三视图如下：
（1）求四棱锥的体积；
（2）求异面直线所成角的大小。