如图,椭圆长轴的端点为A、B,O为椭圆的中心,F为椭圆的右焦点,且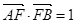 ,
,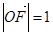 .
.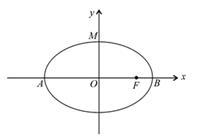
(1)求椭圆的标准方程;
(2)记椭圆的上顶点为M,直线l交椭圆于P,Q两点,问:是否存在直线l,使点F恰为△PQM的垂心,若存在,求出直线l的方程;若不存在,请说明理由.
某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名.为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组:[50,60),[60,70),[70,80),[80,90),[90,100]分别加以统计,得到如图所示的频率分布直方图.
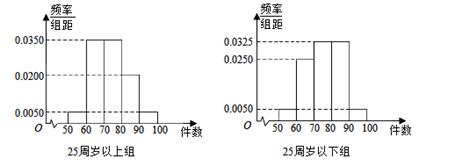
(1)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名“25周岁以下组”工人的频率;
(2)规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成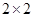 列联表,并判断是否有90%的把握认为“生产能手与工人所在的年龄组有关”?
列联表,并判断是否有90%的把握认为“生产能手与工人所在的年龄组有关”?

(注: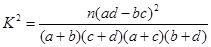 ,n=a+b+c+d)
,n=a+b+c+d)
| |
生产能手 |
非生产能手 |
合计 |
| 25周岁以上组 |
|
|
|
| 25周岁以下组 |
|
|
|
| 合计 |
|
|
|
已知某几何体的三视图和直观图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.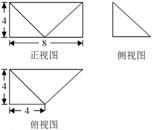

(Ⅰ)求证: ;
;
(Ⅱ)求直线 与平面
与平面 所成角的余弦值;
所成角的余弦值;
(Ⅲ)设 为
为 中点,在棱
中点,在棱 上是否存在一点
上是否存在一点 ,使
,使 平面
平面 ?若存在,求
?若存在,求 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
(1)证明:D1E⊥A1D;
(2)当E为AB的中点时,求点E到面ACD1的距离;
(3)AE等于何值时,二面角D1-EC-D的大小为 .
.
如图,在三棱锥 中,平面
中,平面 平面
平面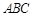 ,
, 为等边三角形,
为等边三角形, ,且
,且 ,O,M分别为
,O,M分别为 ,
, 的中点.
的中点.
(Ⅰ)求证: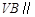 平面
平面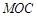 ;
;
(Ⅱ)设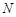 是线段
是线段 上一点,满足平面
上一点,满足平面 平面
平面 ,试说明点的位置
,试说明点的位置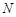 ;
;
(Ⅲ)求三棱锥 的体积.
的体积.
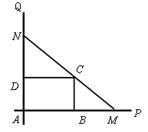
如下图,互相垂直的两条公路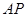 、
、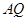 旁有一矩形花园
旁有一矩形花园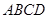 ,现欲将其扩建成一个更
,现欲将其扩建成一个更
大的三角形花园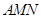 ,要求点
,要求点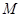 在射线
在射线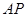 上,点
上,点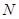 在射线
在射线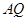 上,且直线
上,且直线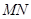 过点
过点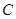 ,其中
,其中 米,
米,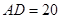 米.记三角形花园
米.记三角形花园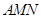 的面积为
的面积为 .
.
(1)问: 取何值时,
取何值时,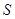 取得最小值,并求出最小值;
取得最小值,并求出最小值;
(2)若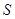 不超过1764平方米,求
不超过1764平方米,求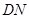 长的取值范围.
长的取值范围.
某校学习小组开展“学生语文成绩与外语成绩的关系”的课题研究,对该校高三年级800名学生上学期期末语文和外语成绩,按优秀和不优秀分类得结果:语文和外语都优秀的有60人,语文成绩优秀但外语成绩不优秀的有140人,外语成绩优秀但语文成绩不优秀的有100人.
(1)能否在犯错概率不超过0.001的前提下认为该校学生的语文成绩和外语成绩有关系?
(2)将上述调查所得到的频率视为概率,从该校高三年级学生成绩中,有放回地随机抽取3名学生的成绩,记抽取的3个成绩中语文、外语两科成绩至少有一科优秀的个数为X,求X的分布列和期望.
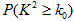 |
0.010 |
0.005 |
0.001 |
 |
6.635 |
7.789 |
10.828 |
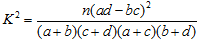
试题篮
()