已知首项都是1的两个数列{an},{bn}(bn≠0,n∈N*)满足anbn+1-an+1bn+2bn+1bn=0.
(1)令cn=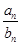 ,求数列{cn}的通项公式;
,求数列{cn}的通项公式;
(2)若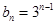 ,求数列{an}的前n项和Sn.
,求数列{an}的前n项和Sn.
巳知二次函数f(x)=ax2+bx+c (a>0,b,c∈R).
(Ⅰ)已知a=2,f(2)=2,若f(x)≥2对x∈R恒成立,求f(x)的表达式;
(Ⅱ)已知方程f(x)=0的两实根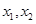 满足
满足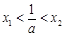 .设f(x)在R上的最小值为m,求证:m<x1.
.设f(x)在R上的最小值为m,求证:m<x1.
已知抛物线C:y2=2px(p>0),曲线M:x2+2x+y2=0(y>0).过点P(-3,0)与曲线M相切于点A的直线l,与抛物线C有且只有一个公共点B.
(Ⅰ)求抛物线C的方程及点A,B的坐标;
(Ⅱ)过点B作倾斜角互补的两条直线分别交抛物线C于S,T两点(不同于坐标原点),求证:直线ST∥直线AO.
设Sn为等差数列{an}的前n项和,其中a1=1,且 ( n∈N*).
( n∈N*).
(Ⅰ)求常数 的值,并写出{an}的通项公式;
的值,并写出{an}的通项公式;
(Ⅱ)记 ,数列{bn}的前n项和为Tn,若对任意的n≥2,都有
,数列{bn}的前n项和为Tn,若对任意的n≥2,都有 成立,求
成立,求 的取值范围.
的取值范围.
如图,三棱锥P-ABC中,E,D分别是棱BC,AC的中点,PB="PC=AB=4,AC=8," BC= ,PA=
,PA= .
.
(Ⅰ)求证:BC⊥平面PED;
(Ⅱ)求直线AC与平面PBC所成角的正弦值.
在△ABC中, 分别是
分别是 的对边长,已知
的对边长,已知 .
.
(Ⅰ)若 ,求实数
,求实数 的值;
的值;
(Ⅱ)若 ,求△ABC面积的最大值.
,求△ABC面积的最大值.
巳知二次函数f(x)=ax2+bx+c (a>0,b,c∈R).设集合A={x∈R| f(x)=x},B={x∈R| f(f(x))= f(x)} ,C={x∈R| f(f(x))="0}" .
(Ⅰ)当a=2,A={2}时,求集合B;
(Ⅱ)若 ,试判断集合C中的元素个数,并说明理由.
,试判断集合C中的元素个数,并说明理由.
已知椭圆C: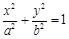 的左顶点为A(-3,0),左焦点恰为圆x2+2x+y2+m=0(m∈R)的圆心M.
的左顶点为A(-3,0),左焦点恰为圆x2+2x+y2+m=0(m∈R)的圆心M.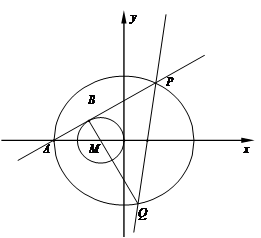
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点A且与圆M相切于点B的直线,交椭圆C于点P,P与椭圆C右焦点的连线交椭圆于Q,若三点B,M,Q共线,求实数 的值.
的值.
设Sn为等差数列{an}的前n项和,其中a1=1,且 ( n∈N*).
( n∈N*).
(Ⅰ)求常数l的值,并写出{an}的通项公式;
(Ⅱ)记 ,数列{bn}的前n项和为Tn,若对任意的
,数列{bn}的前n项和为Tn,若对任意的 (k∈N*),都有
(k∈N*),都有 ,求常数k的最小值.
,求常数k的最小值.
如图,三棱锥P-ABC中,E,D分别是棱BC,AC的中点,PB=PC=AB=4,AC=8,BC= ,PA=
,PA= .
.
(Ⅰ)求证:BC⊥平面PED;
(Ⅱ)求平面PED与平面PAB所成的锐二面角的余弦值.
在△ABC中, 分别是
分别是 的对边长,已知
的对边长,已知 .
.
(Ⅰ)若 ,求实数
,求实数 的值;
的值;
(Ⅱ)若 ,求△ABC面积的最大值.
,求△ABC面积的最大值.
设二次函数 满足条件:①当
满足条件:①当 时,
时, 的最大值为0,且
的最大值为0,且 成立;②二次函数
成立;②二次函数 的图象与直线
的图象与直线 交于
交于 、
、 两点,且
两点,且 .
.
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)求最小的实数 ,使得存在实数
,使得存在实数 ,只要当
,只要当 时,就有
时,就有 成立.
成立.
在数列 中,
中, ,
,
(Ⅰ)求 ,判断数列
,判断数列 的单调性并证明;
的单调性并证明;
(Ⅱ)求证: ;
;
(Ⅲ)是否存在常数 ,对任意
,对任意 ,有
,有 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知直线 与椭圆
与椭圆 相交于
相交于 两个不同的点,记
两个不同的点,记 与
与 轴的交点为
轴的交点为 .
.
(Ⅰ)若 ,且
,且 ,求实数
,求实数 的值;
的值;
(Ⅱ)若 ,求
,求 面积的最大值,及此时椭圆的方程.
面积的最大值,及此时椭圆的方程.
在四棱锥 中,
中, 平面
平面 ,
, 是正三角形,
是正三角形, 与
与 的交点
的交点 恰好是
恰好是 中点,又
中点,又 ,
, ,点
,点 在线段
在线段 上,且
上,且 .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
试题篮
()