已知曲线 的极坐标方程为
的极坐标方程为 ,以极点为原点,极轴为
,以极点为原点,极轴为 轴的正半轴建立平
轴的正半轴建立平
面直角坐标系,设直线 的参数方程为
的参数方程为 (
( 为参数)。
为参数)。
(1)求曲线 的直角坐标方程与直线
的直角坐标方程与直线 的普通方程;
的普通方程;
(2)设曲线 与直线
与直线 相交于
相交于 两点,以
两点,以 为一条边作曲线
为一条边作曲线 的内接矩形,求该矩形的面积。
的内接矩形,求该矩形的面积。
(本小题满分12分)已知 .
.
(1)已知函数h(x)=g(x)+ax3的一个极值点为1,求 的取值;
的取值;
(2) 求函数 在
在 上的最小值;
上的最小值;
(3)对一切 ,
, 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
已知椭圆C的中心在坐标原点,焦点在x轴上,椭圆右顶点到直线 的距离为
的距离为 ,离心率
,离心率
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知A为椭圆与y轴负半轴的交点,设直线 :
: ,是否存在实数m,使直线
,是否存在实数m,使直线 与椭圆有两个不同的交点M、N,是∣AM∣=∣AN∣,若存在,求出 m的值;若不存在,请说明理由。
与椭圆有两个不同的交点M、N,是∣AM∣=∣AN∣,若存在,求出 m的值;若不存在,请说明理由。
某中学为了解学生“掷实心球”项目的整体情况,随机抽取男、女生各20名进行测试,记录的数据如下: 
已知该项目评分标准为:
(Ⅰ)求上述20名女生得分的中位数和众数;
(Ⅱ)从上述20名男生中,有6人的投掷距离低于7.0米,现从这6名男生中随机抽取2名男生,求抽取的2名男生得分都是4分的概率;
(本小题满分12分)已知各项都不相等的等差数列{an}的前7项和为70,且a3为a1和a7的等比中项.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}满足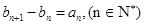 且b1=2,求数列
且b1=2,求数列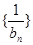 的前n项和Tn。
的前n项和Tn。
已知曲线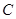 的极坐标方程为
的极坐标方程为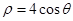 ,以极点为原点,极轴为
,以极点为原点,极轴为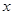 轴的正半轴建立
轴的正半轴建立
平面直角坐标系,设直线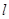 的参数方程为
的参数方程为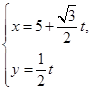 (
(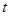 为参数)。
为参数)。
(1)求曲线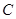 的直角坐标方程与直线
的直角坐标方程与直线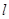 的普通方程;
的普通方程;
(2)设曲线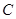 与直线
与直线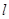 相交于
相交于 两点,以
两点,以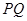 为一条边作曲线
为一条边作曲线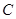 的内接矩形,求该矩形的面积。
的内接矩形,求该矩形的面积。
已知函数f(x)=ex-ax(a为常数)的图像与y轴交于点A,曲线y=f(x)在点A处的切线斜率为-1.
(1)求a的值及函数f(x)的极值;
(2)证明:当x>0时,x2<ex;
(3)证明:对任意给定的正数c,总存在x0,使得当x∈(x0,+∞)时,恒有x2<cex.
已知椭圆C: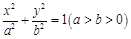 的离心率为
的离心率为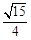 ,
,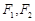 是椭圆的两个焦点,
是椭圆的两个焦点, 是椭圆上任意一点,且
是椭圆上任意一点,且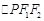 的周长是
的周长是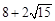 .
.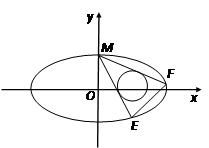
(1)求椭圆C的方程;
(2)设圆T: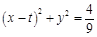 ,过椭圆的上顶点作圆T的两条切线交椭圆于E、F两点,当圆心在
,过椭圆的上顶点作圆T的两条切线交椭圆于E、F两点,当圆心在 轴上移动且
轴上移动且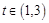 时,求EF的斜率的取值范围.
时,求EF的斜率的取值范围.
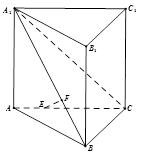
如图,在直三棱柱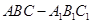 (侧棱和底面垂直的棱柱)中,平面
(侧棱和底面垂直的棱柱)中,平面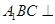 侧面
侧面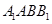 ,
,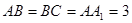 ,线段AC、A1B上分别有一点E、F且满足
,线段AC、A1B上分别有一点E、F且满足 .
.
(1)求证: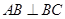 ;
;
(2)求点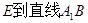 的距离;
的距离;
(3)求二面角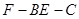 的平面角的余弦值。
的平面角的余弦值。
试题篮
()