如图所示,正方形 所在的平面与等腰
所在的平面与等腰 所在的平面互相垂直,其中顶
所在的平面互相垂直,其中顶 ,
, ,
, 为线段
为线段 的中点.
的中点.
(1)若 是线段
是线段 上的中点,求证:
上的中点,求证: 平面
平面 ;
;
(2)若 是线段
是线段 上的一个动点,设直线
上的一个动点,设直线 与平面
与平面 所成角的大小为
所成角的大小为 ,求
,求 的最大值.
的最大值.
给定函数 和常数
和常数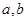 ,若
,若 恒成立,则称
恒成立,则称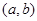 为函数
为函数 的一个“好数对”;若
的一个“好数对”;若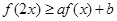 恒成立,则称
恒成立,则称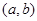 为函数
为函数 的一个“类好数对”.已知函数
的一个“类好数对”.已知函数 的定义域为
的定义域为 .
.
(1)若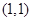 是函数
是函数 的一个“好数对”,且
的一个“好数对”,且 ,求
,求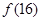 ;
;
(2)若 是函数
是函数 的一个“好数对”,且当
的一个“好数对”,且当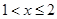 时,
时,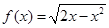 ,求证:
,求证:
函数 在区间
在区间 上无零点;
上无零点;
(3)若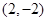 是函数
是函数 的一个“类好数对”,
的一个“类好数对”, ,且函数
,且函数 单调递增,比较
单调递增,比较 与
与 的大小,并说明理由.
的大小,并说明理由.
在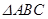 中,角
中,角 ,
, ,
,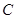 的对边分别为
的对边分别为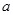 ,
, ,
,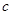 ,已知
,已知 ,
,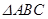 的面积为
的面积为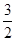 .
.
(1)当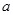 ,
, ,
,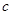 成等差数列时,求
成等差数列时,求 ;
;
(2)求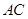 边上的中线
边上的中线 的最小值.
的最小值.
(本小题满分12分)定义 的零点
的零点 为
为 的不动点,已知函数
的不动点,已知函数 .
.
(Ⅰ)当 时,求函数
时,求函数 的不动点;
的不动点;
(Ⅱ)对于任意实数 ,函数
,函数 恒有两个相异的不动点,求实数
恒有两个相异的不动点,求实数 的取值范围;
的取值范围;
(Ⅲ)若函数 只有一个零点且
只有一个零点且 ,求实数
,求实数 的最小值.
的最小值.
某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,得到如下的 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为 。
。
| |
优秀 |
非优秀 |
合计 |
| 甲班 |
10 |
|
|
| 乙班 |
|
30 |
|
| 合计 |
|
|
110 |
(1)请完成上面的列联表;
(2)根据列联表的数据,是否有99.9%的把握认为“成绩与班级有关系”。
参考公式与临界值表: 。
。
 |
0.100 |
0.050 |
0.025 |
0.010 |
0.001 |
 |
2.706 |
3.841 |
5.024 |
6.635 |
10.828 |
试题篮
()