已知函数 (
( 为实数).
为实数).
(Ⅰ)当 时,求函数
时,求函数 的图象在点
的图象在点 处的切线方程;
处的切线方程;
(Ⅱ)设函数 (其中
(其中 为常数),若函数
为常数),若函数 在区间
在区间 上不存在极值,且存在
上不存在极值,且存在 满足
满足
 ,求
,求 的取值范围;
的取值范围;
(Ⅲ)已知 ,求证:
,求证: .
.
已知抛物线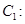
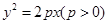 的焦点为
的焦点为 ,抛物线上存在一点
,抛物线上存在一点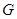 到焦点的距离为
到焦点的距离为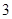 ,且点
,且点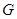 在圆
在圆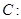
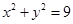 上.
上.
(Ⅰ)求抛物线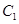 的方程;
的方程;
(Ⅱ)已知椭圆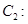
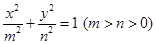 的一个焦点与抛物线
的一个焦点与抛物线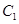 的焦点重合,若椭圆
的焦点重合,若椭圆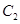 上存在关于直线
上存在关于直线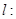
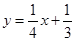 对称的两个不同的点,求椭圆
对称的两个不同的点,求椭圆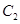 的离心率
的离心率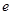 的取值范围.
的取值范围.
设是等差数列,是各项都为正整数的等比数列,且,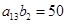 ,
,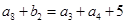 ,
,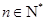 .
.
(Ⅰ)求,的通项公式;
(Ⅱ)若数列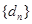 满足
满足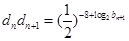 (
(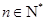 ),且
),且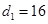 ,试求
,试求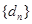 的通项公式及其前
的通项公式及其前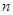 项和
项和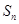 .
.
如图,在正四棱台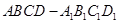 中,
中,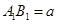 ,
,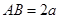 ,
,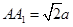 ,
, 、
、 分别是
分别是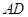 、
、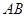 的中点.
的中点. 
(Ⅰ)求证:平面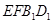 ∥平面
∥平面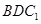 ;
;
(Ⅱ)求二面角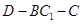 的余弦值的大小.
的余弦值的大小.
注:底面为正方形,从顶点向底面作垂线,垂足是底面中心,这样的四棱锥叫做正四棱锥.用一个平行于正四棱锥底面的平面去截该棱锥,底面与截面之间的部分叫做正四棱台.
为了分流地铁高峰的压力,某市发改委通过听众会,决定实施低峰优惠票价制度.不超过 公里的地铁票价如下表:
公里的地铁票价如下表:
乘坐里程 (单位: (单位: ) ) |
 |
 |
 |
| 票价(单位:元) |
 |
 |
 |
现有甲、乙两位乘客,他们乘坐的里程都不超过 公里.已知甲、乙乘车不超过
公里.已知甲、乙乘车不超过 公里的概率分别为
公里的概率分别为 ,
, ,甲、乙乘车超过
,甲、乙乘车超过 公里且不超过
公里且不超过 公里的概率分别为
公里的概率分别为 ,
, .
.
(Ⅰ)求甲、乙两人所付乘车费用不相同的概率;
(Ⅱ)设甲、乙两人所付乘车费用之和为随机变量 ,求
,求 的分布列与数学期望.
的分布列与数学期望.
已知向量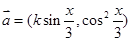 ,
,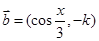 ,实数
,实数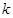 为大于零的常数,函数
为大于零的常数,函数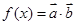 ,
,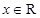 ,且函数
,且函数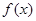 的最大值为
的最大值为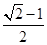 .
.
(Ⅰ)求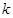 的值;
的值;
(Ⅱ)在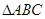 中,
中,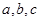 分别为内角
分别为内角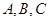 所对的边,若
所对的边,若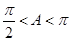 ,
,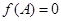 ,且
,且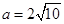 ,求
,求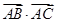 的最小值.
的最小值.
(本小题满分10分)
已知集合A是集合Pn={1,2,3, ,n} (n≥3,n∈N*)的子集,且A中恰有3个元素,同时这3个元素的和是3的倍数.记符合上述条件的集合A的个数为f(n).
(1)求f(3),f(4);
(2)求f(n)(用含n的式子表示).
(本小题满分10分)
如图,四棱锥P-ABCD中,PA^平面ABCD,AD∥BC,AB^AD,BC=,AB=1,BD=PA=2.

(1)求异面直线BD与PC所成角的余弦值;
(2)求二面角A-PD-C的余弦值.
选修4-4:坐标系与参数方程
在极坐标系中,设圆C:r=4 cosq与直线l:q= (r∈R)交于A,B两点,求以AB为直径的圆的极坐标方程.
选修4-2:矩阵与变换
已知矩阵A=,直线l:x-y+4=0在矩阵A对应的变换作用下变为
直线l¢:x-y+2a=0.
(1)求实数a的值;
(2)求A2.
选修4—1:几何证明选讲
如图,AB,AC是⊙O的切线,ADE是⊙O的割线,求证:BE· CD=BD· CE.

(本小题满分16分)
已知数列{an}的各项均为正数,其前n项的和为Sn,且对任意的m,n∈N*,
都有(Sm+n+S1)2=4a2ma2n.
(1)求的值;
(2)求证:{an}为等比数列;
(3)已知数列{cn},{dn}满足|cn|=|dn|=an,p(p≥3)是给定的正整数,数列{cn},{dn}的前p项的和分别为Tp,Rp,且Tp=Rp,求证:对任意正整数k(1≤k≤p),ck=dk.
(本小题满分16分)
已知函数f(x)=x2-x+t,t≥0,g(x)=lnx.
(1)令h(x)=f(x)+g(x),求证:h(x)是增函数;
(2)直线l与函数f(x),g(x)的图象都相切.对于确定的正实数t,讨论直线l的条数,并说明理由.
(本小题满分16分)
在平面直角坐标系xOy中,设中心在坐标原点的椭圆C的左、右焦点分别为F1、F2,右准线
l:x=m+1与x轴的交点为B,BF2=m. 
(1)已知点(,1)在椭圆C上,求实数m的值;
(2)已知定点A(-2,0).
①若椭圆C上存在点T,使得=,求椭圆C的离心率的取值范围;
②当m=1时,记M为椭圆C上的动点,直线AM,BM分别与椭圆C交于另一点P,Q,
若=λ,=m,求证:λ+m为定值.
试题篮
()