(本小题满分12分)为了解甲、乙两校高三年级学生某次期末联考地理成绩情况,从这两学校中分别随机抽取30名高三年级的地理成绩(百分制)作为样本,样本数据的茎叶图如图所示:
(I)若乙校高三年级每位学生被抽取的概率为0.15,求乙校高三年级学生总人数;
(II)根据茎叶图,分析甲、乙两校高三年级学生在这次联考中地理成绩;
(III)从样本中甲、乙两校高三年级学生地理成绩不及格(低于60分为不及格)的学生中随机抽取2人,求至少抽到一名乙校学生的概率.
(本题满分14分)
已知数列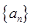 满足
满足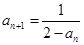 (
( ),
), ,记数列
,记数列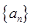 的前
的前 项和为
项和为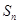 ,
,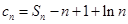 .
.
(I)令 ,求证数列
,求证数列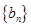 为等差数列,并求其通项公式;
为等差数列,并求其通项公式;
(II)证明: (i)对任意正整数 ,
, 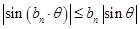 ;
;
(ii)数列 从第2项开始是递增数列.
从第2项开始是递增数列.
(本题满分13分)
设椭圆E:  (
( )过M(2,2e),N(2e,
)过M(2,2e),N(2e,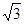 )两点,其中e为椭圆的离心率,
)两点,其中e为椭圆的离心率, 为坐标原点.
为坐标原点.
(I)求椭圆E的方程;
(II)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且 ?若存在,写出该圆的方程;若不存在,说明理由.
?若存在,写出该圆的方程;若不存在,说明理由.
(本题满分12分)
已知四边形 是边长为
是边长为 的菱形,对角线
的菱形,对角线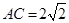 .分别过点
.分别过点 向平面
向平面 外作3条相互平行的直线
外作3条相互平行的直线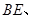
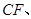
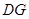 ,其中点
,其中点 在平面
在平面 同侧,
同侧,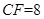 ,且平面
,且平面 与直线
与直线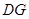 相交于点
相交于点 ,
, ,
,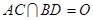 ,连结
,连结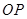 .
.
(I)证明: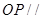
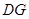 ;
;
(II)当点 在平面
在平面 内的投影恰为
内的投影恰为 点时,求四面体
点时,求四面体 的体积.
的体积.
(本小题满分12分)国家AAAAA级八里河风景区五一期间举办“管仲杯”投掷飞镖比赛.每3人组成一队,每人投掷一次.假设飞镖每次都能投中靶面,且靶面上每点被投中的可能性相同.某人投中靶面内阴影区域记为“成功”(靶面正方形 如图所示,其中阴影区域的边界曲线近似为函数
如图所示,其中阴影区域的边界曲线近似为函数 的图像).每队有3人“成功” 获一等奖,2人“成功” 获二等奖,1人“成功” 获三等奖,其他情况为鼓励奖(即四等奖)(其中任何两位队员“成功”与否互不影响).
的图像).每队有3人“成功” 获一等奖,2人“成功” 获二等奖,1人“成功” 获三等奖,其他情况为鼓励奖(即四等奖)(其中任何两位队员“成功”与否互不影响).
( )求某队员投掷一次“成功”的概率;
)求某队员投掷一次“成功”的概率;
( )设
)设 为某队获奖等次,求随机变量
为某队获奖等次,求随机变量 的分布列及其期望.
的分布列及其期望.
(本题满分12分)
已知函数 .
.
(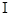 )求函数
)求函数 在
在 上的单调区间;
上的单调区间;
( )在ΔABC中,A为锐角,且角A、B、C所对的边分别为a、b、c,若a=
)在ΔABC中,A为锐角,且角A、B、C所对的边分别为a、b、c,若a= ,
,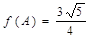 ,求△ABC面积的最大值.
,求△ABC面积的最大值.
定义在 上的函数
上的函数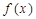 ,如果满足:对任意
,如果满足:对任意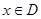 ,存在常数
,存在常数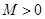 ,都有
,都有
成立,则称 是
是 上的有界函数,其中
上的有界函数,其中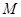 称为函数
称为函数 的上界.已知函数
的上界.已知函数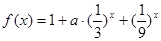 ,
,
(1)当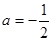 时,求函数
时,求函数 在
在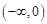 上的值域,并判断函数
上的值域,并判断函数 在
在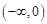 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(2)若函数 在
在 上是以4为上界的有界函数,求实数
上是以4为上界的有界函数,求实数 的取值范围;
的取值范围;
设函数 的最高点
的最高点 的坐标为(
的坐标为( ),由最高
),由最高
点 运动到相邻最低点时,函数图形与
运动到相邻最低点时,函数图形与 轴的交点的坐标为(
轴的交点的坐标为(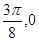 ).
).
(1)求函数 的解析式;
的解析式;
(2)当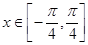 时,求函数
时,求函数 的最大值和最小值以及分别取得最大值和最小值时相应的自变量
的最大值和最小值以及分别取得最大值和最小值时相应的自变量 的值;
的值;
(3)将函数 的图象向右平移
的图象向右平移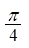 个单位,得到函数
个单位,得到函数 的图象,求函数
的图象,求函数 的单调减区间.
的单调减区间.
试题篮
()