高中数学解答题

在① $\mathit{ac}=\sqrt{3}$，② $c\mathit{sin}A=3$，③ $c=\sqrt{3}b$这三个条件中任选一个，补充在下面问题中，若问题中的三角形存在，求 $c$的值；若问题中的三角形不存在，说明理由．

问题：是否存在 $△\mathit{ABC}$，它的内角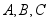的对边分别为 $a,b,c$，且 $\mathit{sin}A=\sqrt{3}\mathit{sin}B$， $C=\frac{\pi }{6}$，________?

注：如果选择多个条件分别解答，按第一个解答计分．

已知椭圆C： $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为 $\frac{\sqrt{2}}{2}$，且过点A（2，1）．

（1）求C的方程：

（2）点M，N在C上，且AM⊥AN，AD⊥MN，D为垂足．证明：存在定点Q，使得|DQ|为定值．

已知函数 $f\left(x\right)=a{e}^{x-1}-\mathit{ln}x+\mathit{ln}a$．

（1）当 $a=e$时，求曲线y=f（x）在点（1，f（1））处的切线与两坐标轴围成的三角形的面积；

（2）若f（x）≥1，求a的取值范围．

如图，四棱锥 P- ABCD的底面为正方形， PD⊥底面 ABCD．设平面 PAD与平面 PBC的交线为 l．

（1）证明： l⊥平面 PDC；

（2）已知 PD= AD=1， Q为 l上的点，求 PB与平面 QCD所成角的正弦值的最大值．

为加强环境保护，治理空气污染，环境监测部门对某市空气质量进行调研，随机抽查了 $100$ 天空气中的 $\mathit{PM}2.5$ 和 $\text{S}{\text{O}}_2$ 浓度（单位： $\mu \text{g/}{\text{m}}^3$ ），得下表：

$\text{S}{\text{O}}_2$ $\mathit{PM}2.5$	$[0,50]$	$(50,150]$	$(150,475]$
$[0,35]$	32	18	4
$(35,75]$	6	8	12
$(75,115]$	3	7	10

（1）估计事件"该市一天空气中 $\mathit{PM}2.5$ 浓度不超过 $75$ ，且 $\text{S}{\text{O}}_2$ 浓度不超过 $150$ "的概率；

（2）根据所给数据，完成下面的 $2\times 2$ 列联表：

$\text{S}{\text{O}}_2$ $\mathit{PM}2.5$	$[0,150]$	$(150,475]$
$[0,75]$
$(75,115]$

（3）根据（2）中的列联表，判断是否有 $99\%$ 的把握认为该市一天空气中 $\mathit{PM}2.5$ 浓度与 $\text{S}{\text{O}}_2$ 浓度有关？

附： $K^2=\frac{n(\mathit{ad}-\mathit{bc}{)}^2}{(a+b)(c+d)(a+c)(b+d)}$ ，

$P(K^2>K)$	0.050	0.010	0.001
K	3.841	6.635	10.828

已知公比大于 $1$的等比数列 $\left\{a_n\right\}$满足 $a_2+a_4=20,a_3=8$．

（1）求 $\left\{a_n\right\}$的通项公式；

（2）记 $b_m$为 $\left\{a_n\right\}$在区间 $(0,m](m\in N^{*})$中的项的个数，求数列 $\left\{b_m\right\}$的前 $100$项和 $S_{100}$．

在① $\mathit{ac}=\sqrt{3}$，② $c\mathit{sin}A=3$，③ $c=\sqrt{3}b$这三个条件中任选一个，补充在下面问题中，若问题中的三角形存在，求 $c$的值；若问题中的三角形不存在，说明理由．

问题：是否存在 $△\mathit{ABC}$，它的内角的对边分别为 $a,b,c$，且 $\mathit{sin}A=\sqrt{3}\mathit{sin}B$， $C=\frac{\pi }{6}$，________?

注：如果选择多个条件分别解答，按第一个解答计分．

已知函数 $f\left(x\right)=\left|x-a^2\right|+|x-2a+1|$ .

（1）当 $a=2$ 时，求不等式 $f\left(x\right)⩾4$ 的解集；

（2）若 $f\left(x\right)⩾4$ ，求 a的取值范围.

已知曲线C₁，C₂的参数方程分别为C₁：（θ为参数），C₂： $\left\{\begin{array}{c}x=t+\frac{1}{t},\\ y=t-\frac{1}{t}\end{array}\right.$（t为参数）.

（1）将C₁，C₂的参数方程化为普通方程；

（2）以坐标原点为极点，x轴正半轴为极轴建立极坐标系.设C₁，C₂的交点为P，求圆心在极轴上，且经过极点和P的圆的极坐标方程.

已知函数f(x)=sin²xsin2x.

（1）讨论f(x)在区间(0，π)的单调性；

（2）证明： $\left|f\left(x\right)\right|\le \frac{3\sqrt{3}}{8}$；

（3）设n∈N*，证明：sin²xsin²2xsin²4x…sin²2ⁿx≤ $\frac{3^n}{4^n}$.

如图，已知三棱柱 ABC- A ₁ B ₁ C ₁的底面是正三角形，侧面 BB ₁ C ₁ C是矩形， M， N分别为 BC， B ₁ C ₁的中点， P为 AM上一点，过 B ₁ C ₁和 P的平面交 AB于 E，交 AC于 F.

（1）证明： AA ₁∥ MN，且平面 A ₁ AMN⊥ EB ₁ C ₁ F；

（2）设 O为△ A ₁ B ₁ C ₁的中心，若 AO∥平面 EB ₁ C ₁ F，且 AO= AB，求直线 B ₁ E与平面 A ₁ AMN所成角的正弦值.

已知椭圆C₁： $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ (a>b>0)的右焦点F与抛物线C₂的焦点重合，C₁的中心与C₂的顶点重合.过F且与x轴垂直的直线交C₁于A，B两点，交C₂于C，D两点，且|CD|= $\frac{4}{3}$|AB|.

（1）求C₁的离心率；

（2）设M是C₁与C₂的公共点，若|MF|=5，求C₁与C₂的标准方程.

某沙漠地区经过治理，生态系统得到很大改善，野生动物数量有所增加.为调查该地区某种野生动物的数量，将其分成面积相近的200个地块，从这些地块中用简单随机抽样的方法抽取20个作为样区，调查得到样本数据(x_i，y_i)(i=1，2，…，20)，其中x_i和y_i分别表示第i个样区的植物覆盖面积(单位：公顷)和这种野生动物的数量，并计算得 $\underset{i=1}{\overset{20}{\sum }}{x}_i=60$， $\underset{i=1}{\overset{20}{\sum }}{y}_i=1200$， $\underset{i=1}{\overset{20}{\sum }}（x_i-\bar{x}{)}^2=80$， $\underset{i=1}{\overset{20}{\sum }}（y_i-\bar{y}{)}^2=9000$， $\underset{i=1}{\overset{20}{\sum }}（x_i-\bar{x})（y_i-\bar{y})=800$.

（1）求该地区这种野生动物数量的估计值（这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数）；

（2）求样本(x_i，y_i)(i=1，2，…，20)的相关系数（精确到0.01）；

（3）根据现有统计资料，各地块间植物覆盖面积差异很大.为提高样本的代表性以获得该地区这种野生动物数量更准确的估计，请给出一种你认为更合理的抽样方法，并说明理由.

附：相关系数r= $\frac{\underset{i=1}{\overset{n}{\sum }}（x_i-\bar{x})（y_i-\bar{y})}{\sqrt{\underset{i=1}{\overset{n}{\sum }}（x_i-\bar{x}{)}^2\underset{i=1}{\overset{n}{\sum }}（y_i-\bar{y}{)}^2}}$，≈1.414.

$△\mathit{ABC}$中，sin²A－sin²B－sin²C=sinBsinC.

（1）求A；

（2）若BC=3，求 $△\mathit{ABC}$周长的最大值.

已知函数 $f\left(x\right)=|3x+1|-2|x-1|$ ．

（1）画出 $y=f\left(x\right)$ 的图像；

（2）求不等式 $f\left(x\right)>f(x+1)$ 的解集．