高中数学解答题

在直角坐标系 $\mathit{xOy}$中，曲线 $C_1$的参数方程为 $(t$为参数 $)$．以坐标原点为极点， $x$轴正半轴为极轴建立极坐标系，曲线 $C_2$的极坐标方程为 $4\rho \mathit{cos}\theta -16\rho \mathit{sin}\theta +3=0$．

（1）当 $k=1$时， $C_1$是什么曲线？

（2）当 $k=4$时，求 $C_1$与 $C_2$的公共点的直角坐标．

已知函数 $f\left(x\right)=e^x+a{x}^2-x$ .

（1）当 a=1时，讨论 f（ x）的单调性；

（2）当 x≥0时， f（ x）≥ $\frac{1}{2}$ x ³+1，求 a的取值范围.

已知A、B分别为椭圆E： $\frac{x^2}{a^2}+y^2=1$（a>1）的左、右顶点，G为E的上顶点， $\overrightarrow{\mathit{AG}}\cdot \overrightarrow{\mathit{GB}}=8$，P为直线x=6上的动点，PA与E的另一交点为C，PB与E的另一交点为D．

（1）求E的方程；

（2）证明：直线CD过定点.

甲、乙、丙三位同学进行羽毛球比赛，约定赛制如下：累计负两场者被淘汰；比赛前抽签决定首先比赛的两人，另一人轮空；每场比赛的胜者与轮空者进行下一场比赛，负者下一场轮空，直至有一人被淘汰；当一人被淘汰后，剩余的两人继续比赛，直至其中一人被淘汰，另一人最终获胜，比赛结束.经抽签，甲、乙首先比赛，丙轮空.设每场比赛双方获胜的概率都为 $\frac{1}{2}$，

（1）求甲连胜四场的概率；

（2）求需要进行第五场比赛的概率；

（3）求丙最终获胜的概率.

如图， $D$ 为圆锥的顶点， $O$ 是圆锥底面的圆心， $\mathit{AE}$ 为底面直径， $\mathit{AE}=\mathit{AD}$ ． $△\mathit{ABC}$ 是底面的内接正三角形， $P$ 为 $\mathit{DO}$ 上一点， $\mathit{PO}=\frac{\sqrt{6}}{6}\mathit{DO}$ ．

（1）证明： $\mathit{PA}\perp$ 平面 $\mathit{PBC}$ ；

（2）求二面角 $B-\mathit{PC}-E$ 的余弦值．

设 $\left\{a_n\right\}$是公比不为1的等比数列， $a_1$为 $a_2$， $a_3$的等差中项．

（1）求 $\left\{a_n\right\}$的公比；

（2）若 $a_1=1$，求数列 $\left\{n{a}_n\right\}$的前 $n$项和．

已知函数 $f\left(x\right)=a{e}^{x-1}-\mathit{ln}x+\mathit{ln}a$．

（1）当 $a=e$时，求曲线y=f（x）在点（1，f（1））处的切线与两坐标轴围成的三角形的面积；

（2）若f（x）≥1，求a的取值范围．

已知椭圆C： $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$过点M（2，3）,点A为其左顶点，且AM的斜率为 $\frac{1}{2}$ ，

（1）求C的方程；

（2）点N为椭圆上任意一点，求△AMN的面积的最大值.

如图，四棱锥 P- ABCD的底面为正方形， PD⊥底面 ABCD．设平面 PAD与平面 PBC的交线为 l．

（1）证明： l⊥平面 PDC；

（2）已知 PD= AD=1， Q为 l上的点，求 PB与平面 QCD所成角的正弦值的最大值．

为加强环境保护，治理空气污染，环境监测部门对某市空气质量进行调研，随机抽查了 $100$ 天空气中的 $\mathit{PM}2.5$ 和 $\text{S}{\text{O}}_2$ 浓度（单位： $\mu \text{g/}{\text{m}}^3$ ），得下表：

$\text{S}{\text{O}}_2$ $\mathit{PM}2.5$	$[0,50]$	$(50,150]$	$(150,475]$
$[0,35]$	32	18	4
$(35,75]$	6	8	12
$(75,115]$	3	7	10

（1）估计事件"该市一天空气中 $\mathit{PM}2.5$ 浓度不超过 $75$ ，且 $\text{S}{\text{O}}_2$ 浓度不超过 $150$ "的概率；

（2）根据所给数据，完成下面的 $2\times 2$ 列联表：

$\text{S}{\text{O}}_2$ $\mathit{PM}2.5$	$[0,150]$	$(150,475]$
$[0,75]$
$(75,115]$

（3）根据（2）中的列联表，判断是否有 $99\%$ 的把握认为该市一天空气中 $\mathit{PM}2.5$ 浓度与 $\text{S}{\text{O}}_2$ 浓度有关？

附： $K^2=\frac{n(\mathit{ad}-\mathit{bc}{)}^2}{(a+b)(c+d)(a+c)(b+d)}$ ，

$P(K^2\ge k)$	0.050	0.010	0.001
$k$	3.841	6.635	10.828

已知公比大于 $1$的等比数列 $\left\{a_n\right\}$满足 $a_2+a_4=20,a_3=8$．

（1）求 $\left\{a_n\right\}$的通项公式；

（2）求 $a_1{a}_2-a_2{a}_3+\dots +(-1{)}^{n-1}{a}_n{a}_{n+1}$.

在① $\mathit{ac}=\sqrt{3}$，② $c\mathit{sin}A=3$，③ $c=\sqrt{3}b$这三个条件中任选一个，补充在下面问题中，若问题中的三角形存在，求 $c$的值；若问题中的三角形不存在，说明理由．

问题：是否存在 $△\mathit{ABC}$，它的内角的对边分别为 $a,b,c$，且 $\mathit{sin}A=\sqrt{3}\mathit{sin}B$， $C=\frac{\pi }{6}$，________?

注：如果选择多个条件分别解答，按第一个解答计分．

甲口袋中装有2个黑球和1个白球，乙口袋中装有3个白球．现从甲、乙两口袋中各任取一个球交换放入另一口袋，重复n次这样的操作，记甲口袋中黑球个数为X_n，恰有2个黑球的概率为p_n，恰有1个黑球的概率为q_n．

（1）求p₁·q₁和p₂·q₂；

（2）求2p_n+q_n与2p_n-1+q_n-1的递推关系式和X_n的数学期望E(X_n)(用n表示) ．

在三棱锥 A- BCD中，已知 CB= CD= $\sqrt{5}$ , BD=2， O为 BD的中点， AO⊥平面 BCD， AO=2， E为 AC的中点．

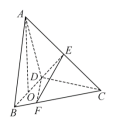
（1）求直线 AB与 DE所成角的余弦值；

（2）若点 F在 BC上，满足 BF= $\frac{1}{4}$ BC，设二面角 F- DE- C的大小为 θ，求sin θ的值．

设，解不等式 $2|x+1|+\left|x\right|\le 4$．