已知 {an}为等比数列, a2a4a5=a3a6, a9a10=-8,则 a7=_____.
若 x, y满足约束条件 {x-3y≤-1x+2y≤93x+y≥7,则 z=2x-y的最大值为_____.
已知 ⊙O的半径为 1,直线 PA与 ⊙O相切于点 A,直线 PB与 ⊙O交于 B, C两点, D为 BC的中点,若 |PO|=√2,则 →PA·→PD的最大值为( )
| A. |
1+√22 |
B. |
1+2√22 |
C. |
1+√2 |
D. |
2+√2 |
设 A, B为双曲线 x2-y29=1上两点,下列四个点中,可为线段 AB中点的是( )
| A. |
(1,1) |
B. |
(-1,2) |
C. |
(1,3) |
D. |
(-1,-4) |
已知等差数列 {an}的公差为 2π3,集合 S={cosann∈N*},若 S={a,b},则 ab=( )
| A. |
-1 |
B. |
-12 |
C. |
0 |
D. |
12 |
已知 △ABC为等腰直角三角形, AB为斜边, △ABD为等边三角形,若二面角 C-AB-D为 150°,则直线 CD与平面 ABC所成角的正切值为( )
| A. |
15 |
B. |
√25 |
C. |
√35 |
D. |
25 |
已知圆锥 PO的底面半径为 √3, O为底面圆心, PA, PB为圆锥的母线, ∠AOB=120°,若 △PAB的面积等于 9√34,则该圆锥的体积为( )
| A. |
π |
B. |
√6π |
C. |
3π |
D. |
3√6π |
甲乙两位同学从 6种课外读物中各自选读 2种,则这两人选读的课外读物中恰有 1种相同的选法共有( )
| A. |
30种 |
B. |
60种 |
C. |
120种 |
D. |
240种 |
已知函数 f(x)=sin(ωx+φ)在区间 (π6,2π3)单调递增,直线 x=π6和 x=2π3为函数 y=f(x)的图像的两条对称轴,则 f(-5π12)= ( )
| A. |
-√32 |
B. |
-12 |
C. |
12 |
D. |
√32 |
设 O为平面坐标系的坐标原点,在区域 {(x,y)1≤x2+y2≤4}内随机取一点,记该点为 A,则直线 OA的倾斜角不大于 π4的概率为( )
| A. |
18 |
B. |
16 |
C. |
14 |
D. |
12 |
已知 f(x)=xexeax-1是偶函数,则 a=( )
| A. |
-2 |
B. |
-1 |
C. |
1 |
D. |
2 |
如图,网格纸上绘制的是一个零件的三视图,网格小正方形的边长为 1,则该零件的表面积为( )
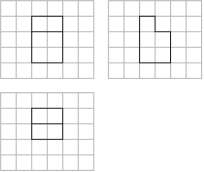
| A. |
24 |
B. |
26 |
C. |
28 |
D. |
30 |
设集合 U=R,集合 M={xx<1}, N={x-1<x<2},则 {xx≥2}=( )
| A. |
CU(M∪N) |
B. |
N∪CUM |
C. |
CU(M∩N) |
D. |
M∪CUN |
试题篮
()