高中物理探究向心力大小与半径、角速度、质量的关系试题

如图所示，小物体A与圆盘保持相对静止，跟着圆盘一起做匀速圆周运动，则A的受力情况是(      )

A．受重力、支持力

B．受重力、支持力和指向圆心的摩擦力

C．重力、支持力、向心力、摩擦力

D．以上均不正确

如图所示，用细线吊着一个质量为m的小球，使小球在水平面内做圆锥摆运动，关于小球受力的说法，正确的是(　　)

A．受重力、拉力、向心力

B．受重力、拉力

C．只受重力

D．以上均不对

下列关于向心力的说法正确的是（   ）

A．物体由于做圆周运动而产生一个向心力

B．做匀速圆周运动的物体，向心力为零

C．向心力只改变物体的运动方向，而不改变物体速度的大小

D．做匀速圆周运动的物体其向心力是不变的

轻杆长L=1.5m，以一端为圆心，在竖直面内做圆周运动，杆另一端固定一个质量m=1.8kg小球，小球通过最高点时速率v=3m/s，求此时小球对杆的作用力大小及方向（g=10m/s²）。

如图所示，有一长为L=0.9m的细线，细线的一端固定在O点，另一端拴一质量为m的小球，现使小球恰好能在竖直面内做完整的圆周运动。已知水平地面上的C点位于O点正下方，且到O点的距离为h=1.9m，不计空气阻力。（g取10m/s²）

（1）求小球通过最高点A时的速度v_A；
（2）若小球通过最低点B时，细线对小球的拉力T恰好为小球重力的6倍，且小球经过B点的瞬间让细线断裂，求小球落地点到C点的距离。

一只小狗拉着雪橇在水平冰面上沿着圆弧形的道路匀速行驶，下图为雪橇受到的牵引力及摩擦力的示意图(O为圆心)，其中正确的是

近几年有些大型的游乐项目很受年青人喜欢,在一些丛林探险的项目中都有滑索过江的体验。若把滑索过江简化成如图的模型，滑索的两端固定，且近似可看成形状固定不变的圆弧，某人从滑索一端滑向另一端的过程中，那么

A．人的运动可看成是匀速圆周运动

B．人在滑到到最低点时处于失重状态

C．人在滑到最低点时重力的瞬时功率最大

D．人在滑到最低点时绳索受到的压力最大

如图所示，一小球从斜轨道的某高度处由静止滑下，然后沿竖直光滑圆轨道的内侧运动，已知圆轨道的半径为R，忽略一切摩擦阻力，则下列说法正确的是

A．在轨道最低点，最高点，轨道对小球作用力的方向是相同的

B．小球的初位置比圆轨道最低点高出2R时，小球能通过圆轨道的最高点

C．小球的初位置比圆轨道最低点高出0.5R时，小球在运动过程中不脱离轨道

D．小球的初位置只有比圆轨道最低点高出2.5R时，小球在运动过程中才能不脱离轨道

近年来我国高速铁路发展迅速，现已知某新型国产机车总质量为m，如图已知两轨间宽度为L，内外轨高度差为h，重力加速度为g，如果机车要进入半径为R的弯道，请问，该弯道处的设计速度最为适宜的是（  ）

A．

B．

C．

D．

狗拉雪橇沿位于水平面内的圆弧形道路匀速行驶，以下给出的四个关于雪橇受到的牵引力F及摩擦力f的示意图（图中O为圆心）中正确的是（ ）

如图所示，一圆盘可绕通过圆盘中心O点且垂直于盘面的竖直轴转动，在圆盘上放置一小木块A，它随圆盘一起做匀速圆周运动，则关于木块A的受力，下列说法正确的是  

A．木块A受重力、支持力

B．木块A受重力、支持力和向心力

C．木块A受重力、支持力和静摩擦力，静摩擦力的方向指向圆心

D．木块A受重力、支持力和静摩擦力，静摩擦力的方向与木块运动方向相反

质量为1000kg的汽车，行驶到一座半径为40m的圆形凸桥顶时，如果汽车队桥的压力恰好为零，则此时汽车所需向心力大小为N，汽车的速度大小为m/s(g取10m/s)

如图所示，一偏心轮绕垂直纸面的轴O匀速转动，a和b是轮上质量相等的两个质点，则偏心轮转动过程中a、b两质点：（    ）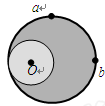

A．角速度大小相同	B．线速度大小相同
C．向心加速度大小相同	D．向心力大小相同

如图所示，长为L的轻杆，一端固定一个质量为m的小球，另一端固定在水平转轴O上，杆随转轴O在竖直平面内匀速转动，角速度为ω，某时刻杆对球的作用力恰好与杆垂直，则此时杆与水平面的夹角θ是 （    ）

A．sinθ=

B．tanθ=

C．sinθ=

D．tanθ=

在冬奥会短道速滑项目中，运动员绕周长仅lll米的短道竞赛。运动员比赛过程中在通过弯道时如果不能很好地控制速度，将发生侧滑而摔离正常比赛路线。图中圆弧虚线Ob代表弯道，即运动正常运动路线，Oa为运动员在O点时的速度方向(研究时可将运动员看作质点)。下列论述正确的是

A．发生侧滑是因为运动员受到的合力方向背离圆心

B．发生侧滑是因为运动员受到的合力大于所需要的向心力

C．若在O点发生侧滑，则滑动的方向在Oa左侧

D．若在O点发生侧滑，则滑动的方向在Oa右侧与Ob之间