高中物理综合题

质量m₁=10g的小球在光滑的水平桌面上以v₁=30cm/s的速率向右运动，恰好遇上在同一条直线上向左运动的另一个小球．第二个小球的质量为m₂=50g，速率v₂=10cm/s．碰撞后，小球m₂恰好停止．那么，碰撞后小球m₁的速度是多大，方向如何？

如图所示质量m=1.0×10^－4kg的小球放在绝缘的水平面上，小球带电量q=2.0×10^－4C，小球与水平面间的动摩擦因数μ=0.2，外加匀强电场E=5V/m,匀强磁场B=2T，方向垂直纸面向外，小球从静止开始运动，求小球的最大加速度和可能达到的最大速度？（g=10m/s）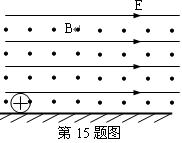

质量为5×10^-6kg的带电粒子以2m/s速度从水平放置的平行金属板A、B中央沿水平方向飞入板间，如图所示.已知板长L＝10cm，间距d＝2cm，当U_AB为1000V时，带电粒子恰好沿直线穿过板间，求该粒子带什么电？电量为多少？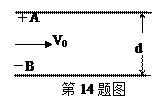

在空间的部分区域中有一水平方向的匀强磁场，磁场的边界如图中的虚线所示。有一矩形线框abcd可以绕竖直的转动轴OOˊ匀角速转动，OOˊ恰好与磁场边界重合。在初始时刻，线框平面与磁场方向平行。已知磁场的磁感强度为B，线框ab边的长度为l，bc边的长度为2l，整个线框的电阻为R，线框转动的角速
度为ω，试求：
（1）线框位于图示位置时，线框中的感应电动势为多大？
（2）线框由图示位置转过30°时，线框受到的安培力矩为多大？

两根相距L=20cm的平行导轨，固定在绝缘板上，倾斜部分与水平方向成α=30⁰角。在导轨的倾斜部分和水平部分分别放两根质量均为m=20g的铜棒，棒与导轨间的动摩擦因数μ=0.25，整个装置放在磁感强度B=0.1T竖直向上的匀强磁场中，如图所示，两根铜棒的总电阻R="0.2Ω," 导轨的电阻不计，求：
（1）cd棒开始运动时的电流多大？
（2）ab棒由斜面顶端静止下滑的速度达到多大时，静止在水平轨道上的cd棒才开始运动？

半径为r的光滑圆环固定在竖直平面内，竖直向下的匀强电场强度为E，与圆环所在平面垂直的匀强磁场的磁感强度为B。一质量为m，带正电量为q的球套在光滑圆环上，从A点由静止开始运动，求小球到达最低位置C（∠AOC=90⁰）时：
（1）小球的速率；
（2）小球对圆环压力的大小。

如图所示，O为一水平轴。细绳上端固定于O轴，下端系一质量m=1.0kg的小球，原来处于静止状态，摆球与平台的B点接触，但对平台无压力，摆长为=0.6m。平台高BD=0.80m。一个质量为M=2.0kg的小球沿平台自左向右运动到B处与摆球发生正碰，碰后摆球在绳的约束下做圆周运动，经最高点A时，绳上的拉力T恰好等于摆球的重力，而M落在水平地面的C点，DC=1.2m。求：质量为M的小球与摆球碰撞前的速度大小(不计空气阻力，取g=10m/s²)。

如图所示，已知正方形abcd边长为，e是cd边的中点，abcd所围区域内是一个磁感应强度大小为B、方向垂直于纸面的匀强磁场，一带电粒子从静止开始经电压为U的电场加速后从a点沿ab方向射入磁场，最后恰好从e点射出。不计带电粒子的重力。求：
(1)带电粒子的电量与质量的比值q/m；
(2)带电粒子从a点到e点的运动时间。
（已知ｓｉｎ５３^ｏ＝０．８　ｃｏｓ５３^ｏ＝０．６　ｔａｎ２６．５^ｏ＝）

如图，水平放置的矩形金属框架，宽0.2米，上面放置一根不计电阻的直导线AB。框架电阻不计，R₁＝2Ω，R₂＝2Ω，B＝0.5T，当AB以10m/s速度向右匀速滑动时，试求：（1）通过R₁、R₂电流的大小和方向
（2）R₁上消耗的电功率

两条金属导轨上水平放置一根导电棒ab，处于竖直向上的匀强磁场中，如图所示，导电棒质量为1.2kg，长1m。当导电棒中通入3A电流时，它可在导轨上匀速滑动，若电流强度增大为5A时，导电棒可获得2m/s²的加速度，求装置所在处的磁感强度的大小。

如图所示，一弹簧振子在A、B间做简谐运动，O点为平衡位置，A、B间的距离为10cm，由A运动到B所需的时间为2s.取向左为正方向，从某时刻开始计时，经1s，振子具有正向的最大加速度。试作出振子的振动图象，并写出简谐运动的位移随时间变化的关系式.

高压锅的锅盖通过几个牙齿似的锅齿与锅镶嵌旋紧，锅盖与锅之间有橡皮制的密封圈，不会漏气.锅盖中间有一排气孔，上面可套上类似砝码的限压阀将排气孔堵住.当加热高压锅（锅内有水），锅内气体压强增加到一定程度时，气体就把限压阀顶起来，蒸汽即从排气孔排出锅外，已知某高压锅的排气孔的直径为0.4cm，大气压强为1.00×10⁵Pa假设锅内水的沸点与锅内压强关系如图所示，要设计一个锅内最高温度达120℃的高压锅，问需要配一个质量多大的限压阀?

利用油膜法可以粗略测出阿伏加德罗常数，把密度的某种油，用滴管滴出一滴油在水面上形成油膜，已知这滴油的体积为V=0.5×10^－3cm³，形成的油膜面积为S=0.7m²，油的摩尔质量M=0.9kg/mol，若把油膜看成是单分子层，每个油分子看成球形，那么：（1）油分子的直径是多少？（2）由以上数据可粗略测出阿伏加德罗常数N_A是多少？（先列出计算式，再代入数据计算，只要求保留一位有效数字）

试问单摆在偏角很小的情况下做简谐运动？

如图16所示为一列简谐波在t₁=0时刻的图象。此时波中质点M的运动方向沿y轴负方向，且到t₂=0.55s质点M恰好第3次到达y轴正方向最大位移处。试求：
（1）此波向什么方向传播？
（2）波速是多大？
（3）从t₁=0至t₃=1.2s，波中质点N运动的路程和相对于平衡位置的位移分别是多少？