小学数学整数的裂项与拆分解答题

按照规律填上数，造出数墙。

读故事想问题。
在数学上也不乏“此时无声胜有声”的小故事。1903年，在纽约的一次数学报告会上，数学家科勒上了讲台，他没说一句话，知识用粉笔在黑板上写了两个算式，一个是67个2相乘减1，另一个是193707721×761838257287，并演算出结果。两个算式的结果完全相同，这时，全场爆发出经久不息的掌声。这是为什么呢？
因为科勒解决了200年来一直没有弄清的一个问题，即67个2相乘减1的结果是不是质数？现在既然它等于另外另个数的乘积，因此证明67个2相乘再减1不是质数，而是合数。
科勒只作了一个简短的无声的报告，可这是他花了3年中全部星期天的试卷才得出的结论。在这简单算式中所蕴涵的智慧、毅力和努力，比洋洋洒洒的万言报告更具魅力。
请你用数学概念说明为什么67个2相乘再减1的结果不是质数而是合数。

从小到大写出5个质数，使后面的数都比前面的数大12．这样的数有几组？

一条公路上，有一个骑车人和一个步行人，骑车人速度是步行驶速度的3倍，每隔6分钟有一辆公共汽车超过步行人，每隔10分钟有一辆公共汽车超过骑车人，如果公共汽车始发站发车时间隔不变，那么多少分钟发一辆公共汽车？

有一种新型电子闹钟，每到正点和半点都响一次铃，每过9分亮一次灯。如果12点时，它既响了铃，又亮了灯，那么下一次既响铃又亮灯是什么时间？

甲乙丙三个互相咬合的齿轮，若使甲轮转5圈时，乙轮转8圈；若乙轮转4圈时，丙轮转7圈。问：这三个齿轮的齿数最少有几个？

有一对互相咬合的齿轮，大齿轮有28个齿，小齿轮有20个齿。大小两个齿轮的某两个齿从第一相遇到第二次相遇（转动的齿轮总数相同），大小两个齿轮各转了 多少圈？

现在有足够数量的1角、5角及1元的硬币若干，如果想用这些硬币组成价值为20元的面额，那么一共有多少种不同的组合方法？

从1～50这50个自然数中选取两个数字，使它们的和大于50，共有多少种不同的取法？

用9，7，0，5，2，0六个数字写数，每个数字只能用一次
最大的六位数：
最小的六位数：
只能读一个零的最大六位数：
只能读两个零的最小六位数：
一个零都不能读的六位数：

一个两位数乘以5，所得的积的结果是一个三位数，且这个三位数的个位与百位数字的和恰好等于十位上的数字．问一共有多少个这样的数?

某住宅区有12家住户，他们的门牌号分别是1，2，…，12．他们的电话号码依次是12个连续的六位自然数，并且每家的电话号码都能被这家的门牌号整除，已知这些电话号码的首位数字都小于6，并且门牌号是9的这一家的电话号码也能被13整除，问：这一家的电话号码是什么数？

泗阳县位于洪泽湖北岸，陆地面积1004平方千米，有丰富的水面养殖资源，水域面积465平方千米，可开发水面养殖资源415平方千米，现已经开发利用60%，县内高渡镇水面养殖资源最为丰富，2003年仅螃蟹养殖面积达108平方米，年创产值8846000元。
（1）横线上的数读作                   ，四舍五入到万位，约是             万
（2）高渡镇螃蟹养殖面积占泗阳县可开发水面养殖资源面积的百分之几？（百分号前保留整数）
（3）泗阳县水面养殖资源开发潜力很大，可开发但尚未开发的水面养殖资源约有多少平方千米？

如图，显微镜下的细菌大约有多少个？

2008年8月24日，第29届奥运会在北京圆满落下帷幕．为了奥运各项赛事的顺利进行，在北京、上海、青岛新建或改建了一系列奥运场馆：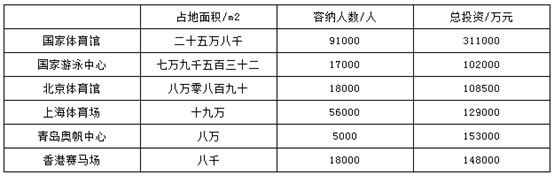

⑴用数字表示各体育馆的占地面积。
⑵把总投资数四舍五入到亿元。