某自行车厂计划每天平均生产n辆自行车，而实际产量与计划产量相比有出入．下表记录了某周五个工作日每天实际产量情况（超过计划产量记为正、少于计划产量记为负）：
| 星期 |
一 |
二 |
三 |
四 |
五 |
| 实际生产量 |
+5 |
﹣2 |
﹣4 |
+13 |
﹣3 |
（1）用含n的代数式表示本周前三天生产自行车的总数；
（2）该厂实行每日计件工资制，每生产一辆车可得60元，若超额完成任务，则超过部分每辆另奖15元；少生产一辆扣20元，当n=100时，那么该厂工人这一周的工资总额是多少元？
（3）若将上面第（2）问中“实行每日计件工资制”改为“实行每周计件工资制”，其他条件不变，当n=100时，在此方式下这一周工人的工资与按日计件的工资哪一个更多？请说明理由．
列式并计算：
（1）﹣1减去
的差乘以﹣7的倒数的积；
（2）﹣2、5、﹣9这三个数的和的绝对值比这三个数的绝对值的和小多少？
已知a的相反数为-2，b的倒数为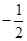
，c的绝对值为2，求a+b+c2的值．
我们规定“*”是一种数学运算符号，两数A、B通过“*”运算得（A+2）×2-B，即A*B=（A+2）×2-B，例如，3*5=（3+2）×2-5=5
（1）求6*7的值；
（2）6*7的值与7*6的值相等吗？
如果a，b互为相反数，c，d互为倒数，m的绝对值为2，那么
+m-cd的值为 ．
A，B，C，D，E五个景点之间的路线如图所示．若每条路线的里程a（km）及行驶的平均速度b（km/h）用（a，b）表示，则从景点A到景点C用时最少的路线是 （ ）
| A．A→E→C | B．A→B→C | C．A→E→B→C | D．A→B→E→C |
某市区自2014年1月起，居民生活用水开始实行阶梯式计量水价，该阶梯式计量水价分为三级（如下表所示）：
| 月用水量（吨） |
水价（元/吨） |
| 第一级 20吨以下（含20吨） |
1．6 |
| 第二级 20吨﹣30吨（含30吨） |
2．4 |
| 第三级 30吨以上 |
3．2 |
例：某用户的月用水量为32吨，按三级计量应缴水费为：
1．6×20＋2．4×10＋3．2×2＝62．4（元）
（1）如果甲用户的月用水量为12吨，则甲需缴的水费为 元；
（2）如果乙用户缴的水费为39．2元，则乙月用水量 吨；
（3）如果丙用户的月用水量为a吨，则丙用户该月应缴水费多少元？（用含a的代数式表示，并化简）
出租车司机小李某天下午的营运全是在东西走向的城中路上进行的，如果规定向东行驶为正，他这天下午行车的里程（单位：千米）如下：＋8， －7， ＋10， －6，＋3，－5，＋9，－6
（1）小李下午出发地记为0，他将最后一名乘客送抵目的地时，小李在出发地的什么方向？距下午出发地有多远？
（2）如果汽车耗油量为0．5升/千米，油箱容量为26升，若出发时油箱装满汽油，请你判断途中是否需要补充汽油？
有一批水果，包装质量为每筐25千克，现抽取8筐样品进行检测，结果称重如下（单位：千克）：27，24，23，28，21，26，22，27，为了求得8筐样品的总质量，我们可以选取的一个恰当的基准数进行简化运算．
（1）你认为选取的一个恰当的基准数为 ；
（2）根据你选取的基准数，用正、负数填写上表；
| 原质量 |
27 |
24 |
23 |
28 |
21 |
26 |
22 |
27 |
| 与基准数的差距 |
|
|
|
|
|
|
|
|
（3）这8筐水果的总质量是多少？
出租车司机小傅某天下午营运全是在东西走向的大道上行驶的．若如果规定向东为正，则行车里程（单位：km）如下：
＋11，－2，＋3，＋10，－11，＋5，－15，－8
（1）当把最后一名乘客送到目的地时，小傅距离出车地点的距离为多少？
（2）若每千米的营运额为7元，成本为1．5元/km，则这天下午他盈利多少元？
观察下列式子：
；
；
；……．
（1）请写出第4个等式： ；
（2）请写出第n个等式 ；
国庆放假时，小红一家三口一起乘小轿车去乡下探望爷爷、奶奶和外公、外婆．早上从家里出发，向东走了6千米到超市买东西，然后又向东走了1．5千米到爷爷家，中午从爷爷家出发向西走了12千米到外公家，晚上返回家里．
（1）若以家为原点，向东为正方向，用1个单位长度表示1千米，请将超市、爷爷家和外公家的位置在下面数轴上分别用点A、B、C表示出来；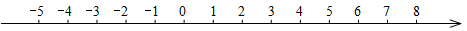
（2）问超市A和外公家C相距多少千米？
（3）若小轿车每千米耗油0．08升，求小红一家从出发到返回家所经历路程小车的耗油量．
观察下列等式，探究其中的规律：
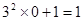
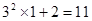
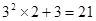
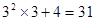
（1）根据以上观察，计算：①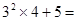 
②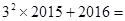 
（2）猜想：当n为自然数时，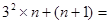
试题篮
()
粤公网安备 44130202000953号
的值是（ ）．
