初中数学计算器—基础知识试题

点(一2．1)所在的象限是(   )

A．第一象限

B．第二象限

C．第三象限

D．第四象限

如图，矩形OABC的边OA、OC分别在x轴、y轴上，点B的坐标为（3，2）．
点D、E分别在AB、BC边上，BD=BE=1．沿直线DE将△BDE翻折，点B落在点B′处．则点B′的坐标为

A．（1，2）．

B．（2，1）．

C．（2，2）．

D．（3，1）．

如图，△ABC的顶点都在正方形网格格点上，点A的坐标为(-1，4). 将△ABC
沿y轴翻折到第一象限，则点C的对应点C′的坐标是  ▲  .

在平面直角坐标系中，点P从原点O出发，每次向上平移2个单位长度或向右平移1个单位长度．
（1）实验操作：在平面直角坐标系中描出点P从点O出发，平移1次后，2次后，3次后可能到达的点，并把相应点的坐标填写在表格中：

（2）观察发现：任一次平移，点P可能到达的点在我们学过的一种函数的图象上，如：平移1次后在函数               的图象上；平移2次后在函数              的图象上……由此我们知道，平移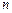次后在函数              的图象上．（请填写相应的解析式）
（3）探索运用：点P从点O出发经过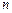次平移后，到达直线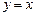上的点Q，且平移的路径长不小于50，不超过56，求点Q的坐标．

火车匀速通过隧道时，火车在隧道内的长度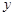（米）与火车行驶时间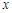（秒）之间的关系用图象描述如图所示，有下列结论：
①火车的长度为120米；
②火车的速度为30米/秒；
③火车整体都在隧道内的时间为25秒；
④隧道长度为750米．
其中正确的结论是     ．（把你认为正确结论的序号都填上）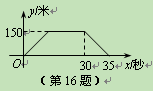

将点P（－2,1）先向左平移1个单位长度，再向上平移2个单位长度得到点P^/,则点P^/的坐标为   ▲   ．

在平面直角坐标系中，点A（2,3）与点B关于轴对称，则点B的坐标为

A．（3,2）

B．（－2，－3）

C．（－2,3）

D．(2,－3)

在直角坐标系中，我们把横、纵坐标都是整数的点叫做整点.且规定，正方形的内部不包含边界上的点.观察如图所示的中心在原点、一边平行于x轴的正方形：边长为1的正方形内部有1个整点，边长为2的正方形内部有1个整点，边长为3的正方形内部有9个整点，…则边长为8的正方形内部的整点的个数为

A．64.

B．49.

C．36.

D．25.

如图，某运动员P从半圆跑道的A点出发沿匀速前进到达终点B，若以时间t为自变量，扇形OAP的面积S为函数的图象大致是（　　）
 

如图4，在长形中截取两个相同的圆作为圆柱的上、下底面，剩余的矩形作为圆
住的侧面，刚好能组合成圆住.设矩形的长和宽分别为y和x，则y与x的函数图象大致是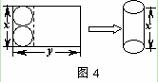

函数y＝中，自变量x的取值范围是          ．

在平面直角坐标系中，点(1,3)位于第       象限．

函数的定义域是_____________．

函数y=中，自变量x的取值范围是           .

向最大容量为60升的热水器内注水，每分钟注水10升，注水2分钟后停止1
分钟，然后继续注水，直至注满.则能反映注水量与注水时间函数关系的图象是   (      )