如图,A,B,C,D为圆O的四等分点,动点P从圆心O出发,沿O—C—D—O—C—D—O路线作匀速运动,设运动时间为x(秒),∠APB的度数为y(度),右图函数图象表示y与x之间函数关系,则点M的横坐标应为
| A.2 | B.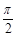 |
C. |
D.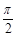 +3 +3 |
如图,正方形ABCD的边长为4,点E,F分别为边AB,BC上的动点,且DE=DF.若△DEF的面积为y,BF的长为x,则表示y与x的函数关系的图象大致是( )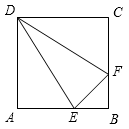
A.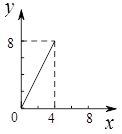 |
B.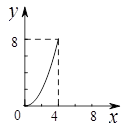 |
C.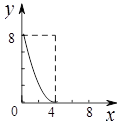 |
D.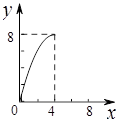 |
在平面直角坐标系中横、纵坐标均是整数的点称为整点,例如点(-1,4)是一个整点.直线y=-x+4与两坐标轴围成△AOB,点P是△AOB的边及其内部的整点,则点P落在以O为圆心,3为半径的圆内的概率为 .
使函数 有意义的自变量x的取值范围为( )
有意义的自变量x的取值范围为( )
| A.x≠0 | B.x≥-1 | C.x≥-1且x≠0 | D.x>-1且x≠0 |
在平面直角坐标系中,四边形OABC是矩形,点B的坐标为(4,3).平行于对角线AC的直线m从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与矩形OABC的两边分别交于点M,N,直线m运动的时间为t(秒).设△OMN的面积为S,则能反映S与t之间函数关系的大致图象是( )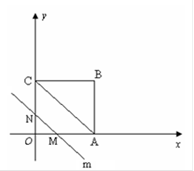
A.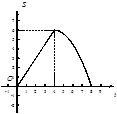 |
B.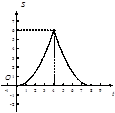 |
C.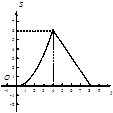 |
D. |
2014年3月31日凌晨,重庆东水门长江大桥正式通车,重庆主城再添一座跨江大桥,为重庆的经济发展提供了帮助.王大爷为了感受重庆交通的发展,搭乘公交车从家去参观东水门长江大桥,预计1个小时能到达.行驶了半个小时,刚好行驶了一半路程,遇到堵车道路被“堵死”,堵了几分钟突然发现旁边刚好有一个轻轨站,于是王大爷转乘轻轨去观看大桥(轻轨速度大于公交车速度),结果按预计时间到达.下面能反映王大爷距大桥的距离y(千米)与时间x(小时)的函数关系的大致图象是( )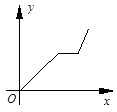
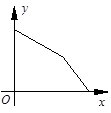
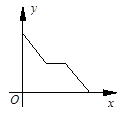
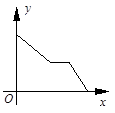
A. B. C. D.
如图1,E为矩形ABCD边AD上一点,点P从点B沿折线BE-ED-DC运动到点C时停止,点Q从点B沿BC运动到点C时停止,它们运动的速度都是1cm/s.若P,Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2).已知y与t的函数图象如图2,则下列结论错误的是( )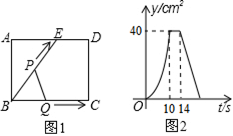
A.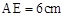 |
B.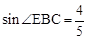 |
C.当0<t≤10时,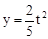 |
D.当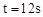 时,△PBQ是等腰三角形 时,△PBQ是等腰三角形 |
已知动点P以每秒2cm的速度沿如图所示的边框按从B⇒C⇒D⇒E⇒F⇒A的路径移动,相应的△ABP的面积S关于时间t的函数图象如图所示,若AB=6cm,试回答下列问题:
(1)动点P在线段 上运动的过程中△ABP的面积S保持不变.
(2)BC= cm; CD= cm; DE= cm; EF= cm
(3)求出图乙中的a与b的值.
已知等腰三角形的周长为24cm,腰长为x(cm),底边为y(cm),则底边y与x的函数关系式为 ,自变量x的取值范围是 .
试题篮
()